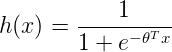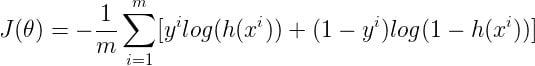Unlock the full potential of your data with the power of data visualization! Go through this blog and discover why visualizations are crucial in Data Science and explore the most effective and game-changing types of visualizations that will revolutionize the way you interpret and extract insights from your data. Get ready to take your data analysis skills to the next level!
What is data visualization?
Data visualization involves using different charts, graphs, and other visual elements to represent data and information graphically and the purpose of it is to make complex and hard to understand and complex datasets easily understandable, accessible, and interpretable.
This powerful tool enables businesses to explore, analyze and identify trends, patterns and relationships from the raw data that are usually hidden by just looking at the data itself or its statistics.
Data visualization guide
By mastering the ability of data visualization, businesses and organizations can make effective and important decisions and actions based on the data and the insights gained. These decisions are additionally referred to as ‘Data-Driven Decisions’. By presenting data in a visual format, analysts can effectively communicate their findings to their team and to their clients, which is a challenging task as clients sometimes can’t interpret raw data and need a medium that they can interpret easily.
Importance of data visualization
Here is a list of some benefits data visualization offers that make us understand its importance and its usefulness:
1. Simplifying complex data: It enables complex data to be presented in a simplified and understandable manner. By using visual representations such as graphs and charts, data can be made more accessible to individuals who are not familiar with the underlying data.
2. Enhancing insights: It can help to identify patterns and trends that might not be immediately apparent from raw data. By presenting data visually, it is easier to identify correlations and relationships between variables, enabling analysts to draw insights and make more informed decisions.
3. Enhanced communication: It makes it easier to communicate complex data to a wider audience, including non-technical stakeholders in a way that is easy to understand and engage with. Visualizations can be used to tell a story, convey complex information, and facilitate collaboration among stakeholders, team members, and decision makers.
4. Increasing efficiency: It can save time and increase efficiency by enabling analysts to quickly identify patterns and relationships in raw data. This can help to streamline the analysis process and enable analysts to focus their efforts on areas that are most likely to yield insights.
5.Identifying anomalies and errors: It can help to identify errors or anomalies in the data. By presenting data visually, it is easier to spot outliers or unusual patterns that might indicate errors in data collection or processing. This can help analysts to clean and refine the data, ensuring that the insights derived from the data are accurate and reliable.
6.Faster and more effective decision-making: It can help you make more informed and data-driven decisions by presenting information in a way that is easy to digest and interpret. Visualizations can help you identify key trends, outliers, and insights that can inform your decision-making, leading to faster and more effective outcomes.
7. Improved data exploration and analysis:It enables you to explore and analyze your data in a more intuitive and interactive way. By visualizing data in different formats and at different levels of detail, you can gain new insights and identify areas for further exploration and analysis.
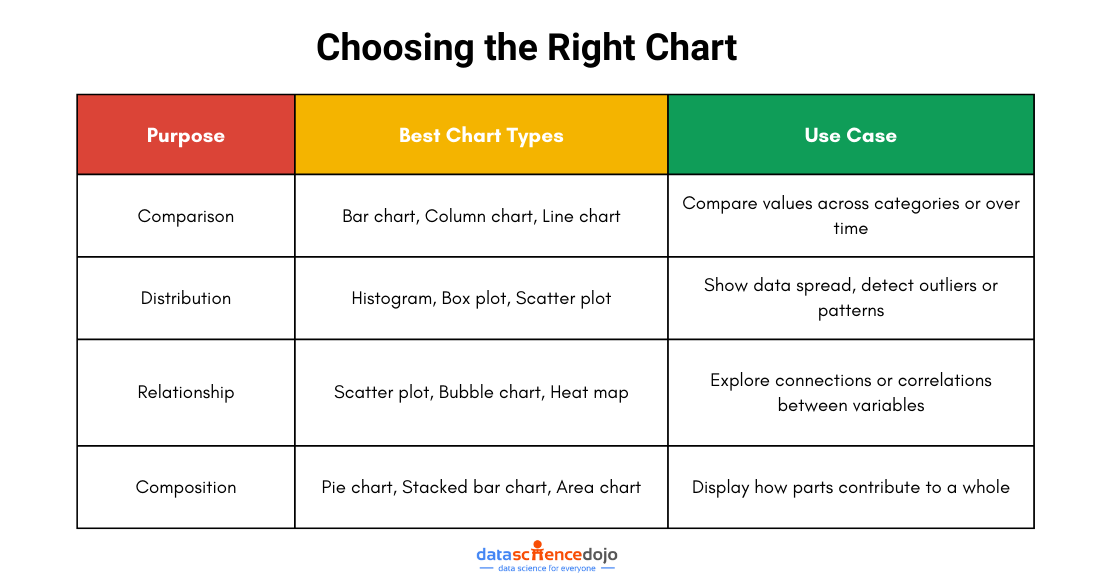
Choosing the right type of visualization
This is the only challenge faced when working with data visualizations, and to master this skill completely, you must have a clear idea about choosing the right type of visual for creating amazing, clear, attractive, and pleasing visuals. Keeping the following points in mind will help you in this:
Identify purpose
Before starting to create your visualization, it’s important to identify what your purpose is. Your purpose may include comparing different values and examining distributions, relationships, or compositions of variables. This step is important as each purpose has a different type of visualization that suits it best.
Understanding audience
You can get help in choosing the best type of visualization for your message if you know about your audience, their preferences, and in which context they will view your visualization. This is useful as different visualizations are more effective with different audiences.
Types of data visualization
Selecting the appropriate visual
Once you have identified your purpose and your audience, the final step is choosing the appropriate visualization to convey your message, some common visuals include:
Comparison Charts: compare different groups/categories.
Distribution Charts: show distributions of a variable.
Relationship Charts: show the relationship between two or more variables.
Composition Charts: show how a whole part is divided into its parts.
Ethics of data visualization & avoiding misleading representations
In many cases, data visualization may also be used to misinterpret information intentionally or unintentionally. An example includes manipulating data by using specific scales or omitting specific data points to support a particular narrative and not showing the actual view of the data. Some considerations regarding the ethics of data visualization include:
Accuracy of data: Data should be accurate and should not be presented in a way to misinterpret information.
Appropriateness of visualization type: The type of visual selected should be appropriate for the data being presented and the message being conveyed.
Clarity of message: The message conveyed through visualization should be clear and easy to understand.
Avoiding bias and discrimination: Each data visualization should be clear of bias and discrimination.
Avoiding misleading representations
You want to represent your data in the most efficient way possible which can be easily interpreted and free of ambiguities, now that’s not always the case, there are times when your data can mislead your visualization and convey the wrong message. In those cases, you can take help from the following points to avoid misleadingness:
Use consistent scales and axes in your charts and graphs.
Avoid using truncated axes and skewed data ranges which cause data to appear less significant.
Label your data points and axes properly for clarity.
Avoid cherry-picking the data to support a particular narrative.
Provide clear and concise context for the data you are presenting.
Types of data visualizations
There are numerous visualizations available, each with its own use and importance, and the choice of a visual depends on your need i.e., what kind of data you want to analyze, and what type of insight are you looking for. Nonetheless, here are some most common visuals used in data science:
Bar Charts:Bar charts are normally used to compare categorical data, such as the frequency or proportion of different categories. They are used to visualize data that can be organized or split into different discrete groups or categories.
Line Graphs: Line graphs are a type of visualization that uses lines to represent data values. They are typically used to represent continuous data.
Scatter Plots: Scatter plot is a type of data visualization that displays the relationship between two quantitative (numerical) variables. They are used to explore and analyze the correlation or association between two continuous variables.
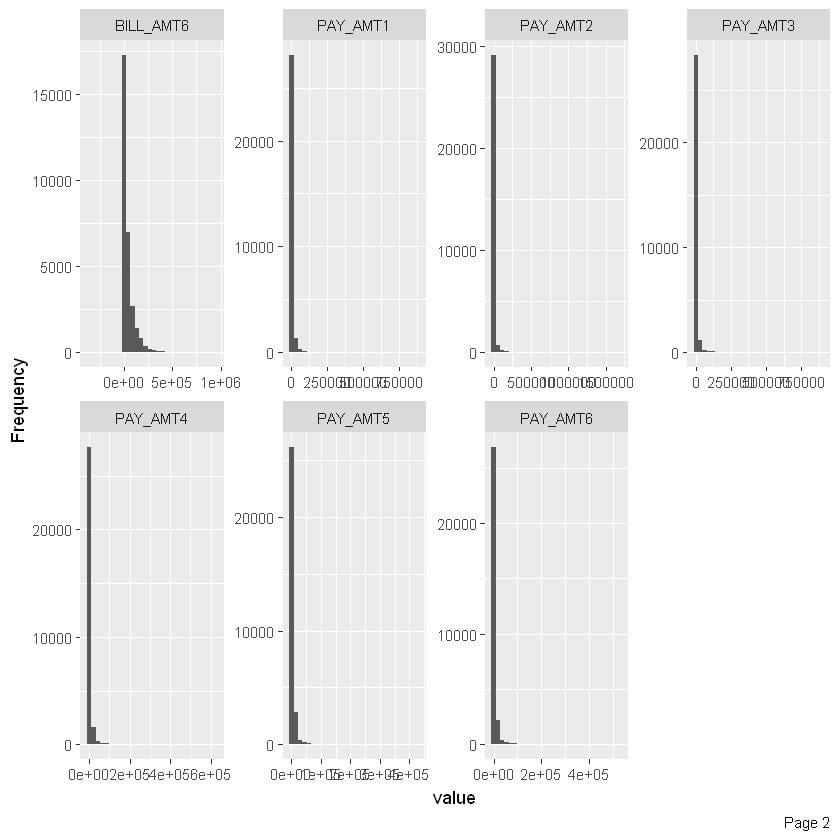
Histograms: A histogram graph represents the distribution of a continuous numerical variable by dividing it into intervals and counting the number of observations. They are used to visualize the shape and spread of data.
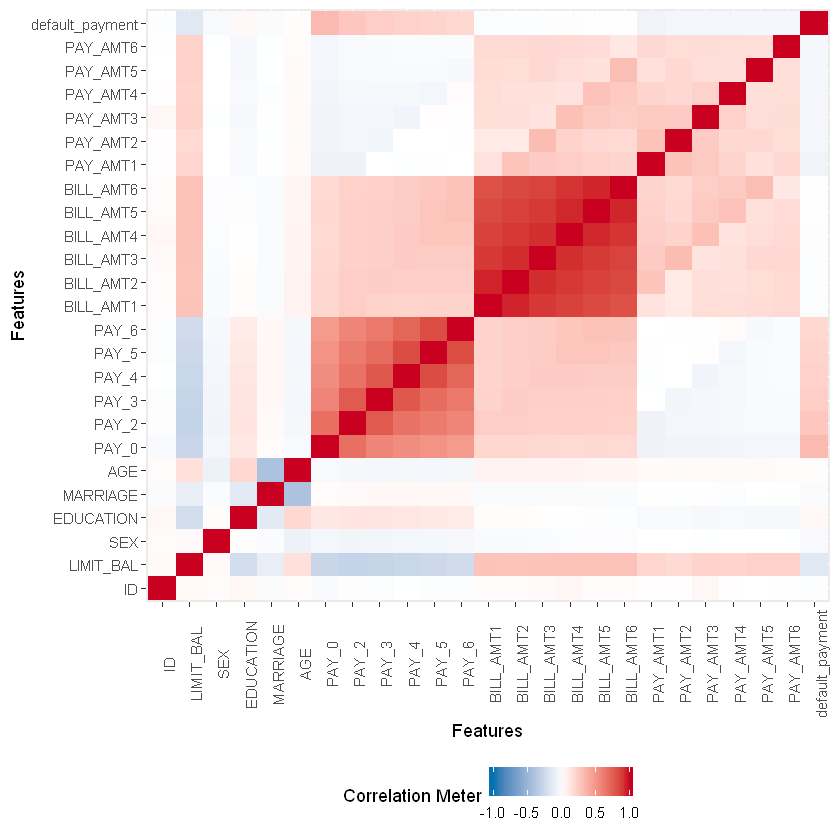
Heatmaps:Heatmaps are commonly used to show the relationships between two variables, such as the correlation between different features in a dataset.
Box and Whisker Plots:They are also known as boxplots and are used to display the distribution of a dataset. A box plot consists of a box that spans the first quartile (Q1) to the third quartile (Q3) of the data, with a line inside the box representing the median.
Count Plots:A count plot is a type of bar chart that displays the number of occurrences of a categorical variable. The x-axis represents the categories, and the y-axis represents the count or frequency of each category.
Point Plots: A point plot is a type of line graph that displays the mean (or median) of a continuous variable for each level of a categorical variable. They are useful for comparing the values of a continuous variable across different levels.
Choropleth Maps:Choropleth map is a type of geographical visualization that uses color to represent data values for different geographic regions, such as countries, states, or counties.
Tree Maps:This visualization is used to display hierarchical data as nested rectangles, with each rectangle representing a node in the hierarchy. Treemaps are useful for visualizing complex hierarchical data in a way that highlights the relative sizes and values of different nodes.
Conclusion
So, this blog was all about introducing you to this powerful tool in the world of data science. Now you have a clear idea about what data visualization is, and what is its importance for analysts, businesses, and stakeholders.
You also learned about how you can choose the right type of visual, the ethics of data visualization and got familiar with 10 new different data visualizations and how they look like. The next step for you is to learn about how you can create these visuals using Python libraries such as matplotlib, seaborn and plotly.
Researchers, statisticians, and data analysts rely on histograms to gain insights into data distributions, identify patterns, and detect outliers. Data scientists and machine learning practitioners use histograms as part of exploratory data analysis and feature engineering. Overall, anyone working with numerical data and seeking to gain a deeper understanding of data distributions can benefit from information on histograms.
Defining histograms
A histogram is a type of graphical representation of data that shows the distribution of numerical values. It consists of a set of vertical bars, where each bar represents a range of values, and the height of the bar indicates the frequency or count of data points falling within that range.
Histograms
Histograms are commonly used in statistics and data analysis to visualize the shape of a data set and to identify patterns, such as the presence of outliers or skewness. They are also useful for comparing the distribution of different data sets or for identifying trends over time.
The picture above shows how 1000 random data points from a normal distribution with a mean of 0 and standard deviation of 1 are plotted in a histogram with 30 bins and black edges.
Advantages of histograms
Visual Representation: Histograms provide a visual representation of the distribution of data, enabling us to observe patterns, trends, and anomalies that may not be apparent in raw data.
Easy Interpretation: Histograms are easy to interpret, even for non-experts, as they utilize a simple bar chart format that displays the frequency or proportion of data points in each bin.
Outlier Identification: Histograms are useful for identifying outliers or extreme values, as they appear as individual bars that significantly deviate from the rest of the bars.
Comparison of Data Sets: Histograms facilitate the comparison of distribution between different data sets, enabling us to identify similarities or differences in their patterns.
Data Summarization: Histograms are effective for summarizing large amounts of data by condensing the information into a few key features, such as the shape, center, and spread of the distribution.
Creating a histogram using Matplotlib library
We can create histograms using Matplotlib by following a series of steps. Following the import statements of the libraries, the code generates a set of 1000 random data points from a normal distribution with a mean of 0 and standard deviation of 1, using the `numpy.random.normal()` function.
The plt.hist() function in Python is a powerful tool for creating histograms. By providing the data, number of bins, bar color, and edge color as input, this function generates a histogram plot.
To enhance the visualization, the xlabel(), ylabel(), and title() functions are utilized to add labels to the x and y axes, as well as a title to the plot.
Finally, the show() function is employed to display the histogram on the screen, allowing for detailed analysis and interpretation.
Overall, this code generates a histogram plot of a set of random data points from a normal distribution, with 30 bins, blue bars, black edges, labeled axes, and a title. The histogram shows the frequency distribution of the data, with a bell-shaped curve indicating the normal distribution.
Customizations available in Matplotlib for histograms
In Matplotlib, there are several customizations available for histograms. These include:
Adjusting the number of bins.
Changing the color of the bars.
Changing the opacity of the bars.
Changing the edge color of the bars.
Adding a grid to the plot.
Adding labels and a title to the plot.
Adding a cumulative density function (CDF) line.
Changing the range of the x-axis.
Adding a rug plot.
Now, let’s see all the customizations being implemented in a single example code snippet:
In this example, the histogram is customized in the following ways:
The number of bins is set to `20` using the `bins` parameter.
The transparency of the bars is set to `0.5` using the `alpha` parameter.
The edge color of the bars is set to `black` using the `edgecolor` parameter.
The color of the bars is set to `green` using the `color` parameter.
The range of the x-axis is set to `(-3, 3)` using the `range` parameter.
The y-axis is normalized to show density using the `density` parameter.
Labels and a title are added to the plot using the `xlabel()`, `ylabel()`, and `title()` functions.
A grid is added to the plot using the `grid` function.
A cumulative density function (CDF) line is added to the plot using the `cumulative` parameter and `histtype=’step’`.
A rug plot showing individual data points is added to the plot using the `plot` function.
Creating a histogram using ‘Seaborn’ library:
We can create histograms using Seaborn by following the steps:
First and foremost, importing the libraries: `NumPy`, `Seaborn`, `Matplotlib`, and `Pandas`. After importing the libraries, a toy dataset is created using `pd.DataFrame()` of 1000 samples that are drawn from a normal distribution with mean 0 and standard deviation 1 using NumPy’s `random.normal()` function.
We use Seaborn’s `histplot()` function to plot a histogram of the ‘data’ column of the DataFrame with `20` bins and a `blue` color.
The plot is customized by adding labels, and a title, and changing the style to a white grid using the `set_style()` function.
Finally, we display the plot using the `show()` function from matplotlib.
Overall, this code snippet demonstrates how to use Seaborn to plot a histogram of a dataset and customize the appearance of the plot quickly and easily.
Customizations available in Seaborn for histograms
Following is a list of the customizations available for Histograms in Seaborn:
Change the number of bins.
Change the color of the bars.
Change the color of the edges of the bars.
Overlay a density plot on the histogram.
Change the bandwidth of the density plot.
Change the type of histogram to cumulative.
Change the orientation of the histogram to horizontal.
Change the scale of the y-axis to logarithmic.
Now, let’s see all these customizations being implemented here as well, in a single example code snippet:
In this example, we have done the following customizations:
Set the number of bins to `20`.
Set the color of the bars to `green`.
Set the `edgecolor` of the bars to `black`.
Added a density plot overlaid on top of the histogram using the `kde` parameter set to `True`.
Set the bandwidth of the density plot to `0.5` using the `kde_kws` parameter.
Set the histogram to be cumulative using the `cumulative` parameter.
Set the y-axis scale to logarithmic using the `log_scale` parameter.
Set the title of the plot to ‘Customized Histogram’.
Set the x-axis label to ‘Values’.
Set the y-axis label to ‘Frequency’.
Limitations of Histograms:
Histograms are widely used for visualizing the distribution of data, but they also have limitations that should be considered when interpreting them. These limitations are jotted down below:
They can be sensitive to the choice of bin size or the number of bins, which can affect the interpretation of the distribution. Choosing too few bins can result in a loss of information while choosing too many bins can create artificial patterns and noise.
They can be influenced by outliers, which can skew the distribution or make it difficult to see patterns in the data.
They are typically univariate and cannot capture relationships between multiple variables or dimensions of data.
Histograms assume that the data is continuous and does not work well with categorical data or data with large gaps between values.
They can be affected by the choice of starting and ending points, which can affect the interpretation of the distribution.
They do not provide information on the shape of the distribution beyond the binning intervals.
It’s important to consider these limitations when using histograms and to use them in conjunction with other visualization techniques to gain a more complete understanding of the data.
Wrapping up
In conclusion, histograms are powerful tools for visualizing the distribution of data. They provide valuable insights into the shape, patterns, and outliers present in a dataset. With their simplicity and effectiveness, histograms offer a convenient way to summarize and interpret large amounts of data.
By customizing various aspects such as the number of bins, colors, and labels, you can tailor the histogram to your specific needs and effectively communicate your findings. So, embrace the power of histograms and unlock a deeper understanding of your data.
Learn how logistic regression fits a dataset to make predictions in R, as well as when and why to use it.
Logistic regression is one of the statistical techniques in machine learning used to form prediction models. It is one of the most popular classification algorithms mostly used for binary classification problems (problems with two class values, however, some variants may deal with multiple classes as well). It’s used for various research and industrial problems.
Therefore, it is essential to have a good grasp of logistic regression algorithms while learning data science. This tutorial is a sneak peek from many of Data Science Dojo’s hands-on exercises from their data science Bootcamp program, you will learn how logistic regression fits a dataset to make predictions, as well as when and why to use it.
In short, Logistic Regression is used when the dependent variable(target) is categorical. For example:
To predict whether an email is spam (1) or not spam (0)
Whether the tumor is malignant (1) or not (0)
Intro to logistic regression
It is named ‘Logistic Regression’ because its underlying technology is quite the same as Linear Regression. There are structural differences in how linear and logistic regression operate. Therefore, linear regression isn’t suitable to be used for classification problems. This link answers in detail why linear regression isn’t the right approach for classification.
Its name is derived from one of the core functions behind its implementation called the logistic function or the sigmoid function. It’s an S-shaped curve that can take any real-valued number and map it into a value between 0 and 1, but never exactly at those limits.
The hypothesis function of logistic regression can be seen below where the function g(z) is also shown.
The hypothesis for logistic regression now becomes:
Here θ (theta) is a vector of parameters that our model will calculate to fit our classifier.
After calculations from the above equations, the cost function is now as follows:
Here m is several training examples. Like Linear Regression, we will use gradient descent to minimize our cost function and calculate the vector θ (theta).
This tutorial will follow the format below to provide you with hands-on practice with Logistic Regression:
Importing Libraries
Importing Datasets
Exploratory Data Analysis
Feature Engineering
Pre-processing
Model Development
Prediction
Evaluation
The scenario
In this tutorial, we will be working with the Default of Credit Card Clients Data Set. This data set has 30000 rows and 24 columns. The data set could be used to estimate the probability of default payment by credit card clients using the data provided. These attributes are related to various details about a customer, his past payment information, and bill statements. It is hosted in Data Science Dojo’s repository.
Think of yourself as a lead data scientist employed at a large bank. You have been assigned to predict whether a particular customer will default on their payment next month or not. The result is an extremely valuable piece of information for the bank to take decisions regarding offering credit to its customers and could massively affect the bank’s revenue. Therefore, your task is very critical. You will learn to use logistic regression to solve this problem.
The dataset is a tricky one as it has a mix of categorical and continuous variables. Moreover, you will also get a chance to practice these concepts through short assignments given at the end of a few sub-modules. Feel free to change the parameters in the given methods once you have been through the entire notebook.
We’ll begin by importing the dependencies that we require. The following dependencies are popularly used for data wrangling operations and visualizations. We would encourage you to have a look at their documentation.
library(knitr)
library(tidyverse)
library(ggplot2)
library(mice)
library(lattice)
library(reshape2)
#install.packages("DataExplorer") if the following package is not available
library(DataExplorer)
2) Importing Datasets
The dataset is available at Data Science Dojo’s repository in the following link. We’ll use the head method to view the first few rows.
## Need to fetch the excel file
path <- "https://code.datasciencedojo.com/datasciencedojo/datasets/raw/master/
Default%20of%20Credit%20Card%20Clients/default%20of%20credit%20card%20clients.csv"
data <- read.csv(file = path, header = TRUE)
head(data)
Since the header names are in the first row of the dataset, we’ll use the code below to first assign the headers to be the one from the first row and then delete the first row from the dataset. This way we will get our desired form.
colnames(data) <- as.character(unlist(data[1,]))
data = data[-1, ]
head(data)
To avoid any complications ahead, we’ll rename our target variable “default payment next month” to a name without spaces using the code below.
colnames(data)[colnames(data)=="default payment next month"] <- "default_payment"
head(data)
3) Exploratory data analysis
Data Exploration is one of the most significant portions of the machine-learning process. Clean data can ensure a notable increase in the accuracy of our model. No matter how powerful our model is, it cannot function well unless the data we provide has been thoroughly processed.
This step will briefly take you through this step and assist you to visualize your data, find the relation between variables, deal with missing values and outliers and assist in getting some fundamental understanding of each variable we’ll use. Moreover, this step will also enable us to figure out the most important attributes to feed our model and discard those that have no relevance.
We will start by using the dim function to print out the dimensionality of our data frame.
dim(data)
30000 25
The str method will allow us to know the data type of each variable. We’ll transform it to a numeric data type since it’ll be handier to use for our functions ahead.
We have involved an intermediate step by converting our data to character first. We need to use as.character before as.numeric. This is because factors are stored internally as integers with a table to give the factor level labels. Just using as.numeric will only give the internal integer codes.
When applied to a data frame, the summary() function is essentially applied to each column, and the results for all columns are shown together. For a continuous (numeric) variable like “age”, it returns the 5-number summary showing 5 descriptive statistic as these are numeric values.
summary(data)
ID LIMIT_BAL SEX EDUCATION
Min. : 1 Min. : 10000 Min. :1.000 Min. :0.000
1st Qu.: 7501 1st Qu.: 50000 1st Qu.:1.000 1st Qu.:1.000
Median :15000 Median : 140000 Median :2.000 Median :2.000
Mean :15000 Mean : 167484 Mean :1.604 Mean :1.853
3rd Qu.:22500 3rd Qu.: 240000 3rd Qu.:2.000 3rd Qu.:2.000
Max. :30000 Max. :1000000 Max. :2.000 Max. :6.000
MARRIAGE AGE PAY_0 PAY_2
Min. :0.000 Min. :21.00 Min. :-2.0000 Min. :-2.0000
1st Qu.:1.000 1st Qu.:28.00 1st Qu.:-1.0000 1st Qu.:-1.0000
Median :2.000 Median :34.00 Median : 0.0000 Median : 0.0000
Mean :1.552 Mean :35.49 Mean :-0.0167 Mean :-0.1338
3rd Qu.:2.000 3rd Qu.:41.00 3rd Qu.: 0.0000 3rd Qu.: 0.0000
Max. :3.000 Max. :79.00 Max. : 8.0000 Max. : 8.0000
PAY_3 PAY_4 PAY_5 PAY_6
Min. :-2.0000 Min. :-2.0000 Min. :-2.0000 Min. :-2.0000
1st Qu.:-1.0000 1st Qu.:-1.0000 1st Qu.:-1.0000 1st Qu.:-1.0000
Median : 0.0000 Median : 0.0000 Median : 0.0000 Median : 0.0000
Mean :-0.1662 Mean :-0.2207 Mean :-0.2662 Mean :-0.2911
3rd Qu.: 0.0000 3rd Qu.: 0.0000 3rd Qu.: 0.0000 3rd Qu.: 0.0000
Max. : 8.0000 Max. : 8.0000 Max. : 8.0000 Max. : 8.0000
BILL_AMT1 BILL_AMT2 BILL_AMT3 BILL_AMT4
Min. :-165580 Min. :-69777 Min. :-157264 Min. :-170000
1st Qu.: 3559 1st Qu.: 2985 1st Qu.: 2666 1st Qu.: 2327
Median : 22382 Median : 21200 Median : 20089 Median : 19052
Mean : 51223 Mean : 49179 Mean : 47013 Mean : 43263
3rd Qu.: 67091 3rd Qu.: 64006 3rd Qu.: 60165 3rd Qu.: 54506
Max. : 964511 Max. :983931 Max. :1664089 Max. : 891586
BILL_AMT5 BILL_AMT6 PAY_AMT1 PAY_AMT2
Min. :-81334 Min. :-339603 Min. : 0 Min. : 0
1st Qu.: 1763 1st Qu.: 1256 1st Qu.: 1000 1st Qu.: 833
Median : 18105 Median : 17071 Median : 2100 Median : 2009
Mean : 40311 Mean : 38872 Mean : 5664 Mean : 5921
3rd Qu.: 50191 3rd Qu.: 49198 3rd Qu.: 5006 3rd Qu.: 5000
Max. :927171 Max. : 961664 Max. :873552 Max. :1684259
PAY_AMT3 PAY_AMT4 PAY_AMT5 PAY_AMT6
Min. : 0 Min. : 0 Min. : 0.0 Min. : 0.0
1st Qu.: 390 1st Qu.: 296 1st Qu.: 252.5 1st Qu.: 117.8
Median : 1800 Median : 1500 Median : 1500.0 Median : 1500.0
Mean : 5226 Mean : 4826 Mean : 4799.4 Mean : 5215.5
3rd Qu.: 4505 3rd Qu.: 4013 3rd Qu.: 4031.5 3rd Qu.: 4000.0
Max. :896040 Max. :621000 Max. :426529.0 Max. :528666.0
default_payment
Min. :0.0000
1st Qu.:0.0000
Median :0.0000
Mean :0.2212
3rd Qu.:0.0000
Max. :1.0000
Using the introduced method, we can get to know the basic information about the dataframe, including the number of missing values in each variable.
introduce(data)
As we can observe, there are no missing values in the dataframe.
The information in summary above gives a sense of the continuous and categorical features in our dataset. However, evaluating these details against the data description shows that categorical values such as EDUCATION and MARRIAGE have categories beyond those given in the data dictionary. We’ll find out these extra categories using the value_counts method.
count(data, vars = EDUCATION)
vars
n
0
14
1
10585
2
14030
3
4917
4
123
5
280
6
51
The data dictionary defines the following categories for EDUCATION: “Education (1 = graduate school; 2 = university; 3 = high school; 4 = others)”. However, we can also observe 0 along with numbers greater than 4, i.e. 5 and 6. Since we don’t have any further details about it, we can assume 0 to be someone with no educational experience and 0 along with 5 & 6 can be placed in others along with 4.
count(data, vars = MARRIAGE)
vars
n
0
54
1
13659
2
15964
3
323
The data dictionary defines the following categories for MARRIAGE: “Marital status (1 = married; 2 = single; 3 = others)”. Since category 0 hasn’t been defined anywhere in the data dictionary, we can include it in the ‘others’ category marked as 3.
count(data, vars = MARRIAGE)
count(data, vars = EDUCATION)
vars
n
1
13659
2
15964
3
377
vars
n
1
10585
2
14030
3
4917
4
468
We’ll now move on to a multi-variate analysis of our variables and draw a correlation heat map from the DataExplorer library. The heatmap will enable us to find out the correlation between each variable. We are more interested in finding out the correlation between our predictor attributes with the target attribute default payment next month. The color scheme depicts the strength of correlation between 2 variables.
This will be a simple way to quickly find out how much an impact a variable has on our final outcome. There are other ways as well to figure this out.
plot_correlation(na.omit(data), maxcat = 5L)
We can observe the week correlation of AGE, BILL_AMT1, BILL_AMT2, BILL_AMT3, BILL_AMT4, BILL_AMT5, BILL_AMT6 with our target variable.
Now let’s have a univariate analysis of our variables. We’ll start with the categorical variables and have a quick check on the frequency of distribution of categories. The code below will allow us to observe the required graphs. We’ll first draw distribution for all PAY variables.
plot_histogram(data)
We can make a few observations from the above histogram. The distribution above shows that all nearly all PAY attributes are rightly skewed.
4) Feature engineering
This step can be more important than the actual model used because a machine learning algorithm only learns from the data we give it, and creating features that are relevant to a task is absolutely crucial.
Analyzing our data above, we’ve been able to note the extremely week correlation of some variables with the final target variable. The following are the ones which have significantly low correlation values: AGE, BILL_AMT2, BILL_AMT3, BILL_AMT4, BILL_AMT5, BILL_AMT6.
Standardization is a transformation that centers the data by removing the mean value of each feature and then scale it by dividing (non-constant) features by their standard deviation. After standardizing data the mean will be zero and the standard deviation one.
It is most suitable for techniques that assume a Gaussian distribution in the input variables and work better with rescaled data, such as linear regression, logistic regression and linear discriminate analysis. If a feature has a variance that is orders of magnitude larger than others, it might dominate the objective function and make the estimator unable to learn from other features correctly as expected.
In the code below, we’ll use the scale method transform our dataset using it.
data_new[, 1:17] <- scale(data_new[, 1:17])
head(data_new)
The next task we’ll do is to split the data for training and testing as we’ll use our test data to evaluate our model. We will now split our dataset into train and test. We’ll change it to 0.3. Therefore, 30% of the dataset is reserved for testing while the remaining for training. By default, the dataset will also be shuffled before splitting.
#create a list of random number ranging from 1 to number of rows from actual data
#and 70% of the data into training data
data2 = sort(sample(nrow(data_new), nrow(data_new)*.7))
#creating training data set by selecting the output row values
train <- data_new[data2,]
#creating test data set by not selecting the output row values
test <- data_new[-data2,]
Let us print the dimensions of all these variables using the dim method. You can notice the 70-30% split.
dim(train)
dim(test)
21000 18
9000 18
6) Model development
We will now move on to our most important step of developing our logistic regression model. We have already fetched our machine learning model in the beginning. Now with a few lines of code, we’ll first create a logistic regression model which as has been imported from sci-kit learn’s linear model package to our variable named model.
Followed by this, we’ll train our model using the fit method with X_train and y_train which contain 70% of our dataset. This will be a binary classification model.
## fit a logistic regression model with the training dataset
log.model <- glm(default_payment ~., data = train, family = binomial(link = "logit"))
summary(log.model)
Call:
glm(formula = default_payment ~ ., family = binomial(link = "logit"),
data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.1171 -0.6998 -0.5473 -0.2946 3.4915
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.465097 0.019825 -73.900 < 2e-16 ***
LIMIT_BAL -0.083475 0.023905 -3.492 0.000480 ***
SEX -0.082986 0.017717 -4.684 2.81e-06 ***
EDUCATION -0.059851 0.019178 -3.121 0.001803 **
MARRIAGE -0.107322 0.018350 -5.849 4.95e-09 ***
PAY_0 0.661918 0.023605 28.041 < 2e-16 ***
PAY_2 0.069704 0.028842 2.417 0.015660 *
PAY_3 0.090691 0.031982 2.836 0.004573 **
PAY_4 0.074336 0.034612 2.148 0.031738 *
PAY_5 0.018469 0.036430 0.507 0.612178
PAY_6 0.006314 0.030235 0.209 0.834584
BILL_AMT1 -0.123582 0.023558 -5.246 1.56e-07 ***
PAY_AMT1 -0.136745 0.037549 -3.642 0.000271 ***
PAY_AMT2 -0.246634 0.056432 -4.370 1.24e-05 ***
PAY_AMT3 -0.014662 0.028012 -0.523 0.600677
PAY_AMT4 -0.087782 0.031484 -2.788 0.005300 **
PAY_AMT5 -0.084533 0.030917 -2.734 0.006254 **
PAY_AMT6 -0.027355 0.025707 -1.064 0.287277
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 22176 on 20999 degrees of freedom
Residual deviance: 19535 on 20982 degrees of freedom
AIC: 19571
Number of Fisher Scoring iterations: 6
7) Prediction
Below we’ll use the prediction method to find out the predictions made by our Logistic Regression method. We will first store the predicted results in our y_pred variable and print our first 10 rows of our test data set. Following this we will print the predicted values of the corresponding rows and the original labels that were stored in y_test for comparison.
test[1:10,]
## to predict using logistic regression model, probablilities obtained
log.predictions <- predict(log.model, test, type="response")
## Look at probability output
head(log.predictions, 10)
2
0.539623162720197
7
0.232835137994762
10
0.25988780274953
11
0.0556716133560243
15
0.422481223473459
22
0.165384552048511
25
0.0494775267027534
26
0.238225423596718
31
0.248366972046479
37
0.111907725985513
Below we are going to assign our labels with decision rule that if the prediction is greater than 0.5, assign it 1 else 0.
We’ll now discuss a few evaluation metrics to measure the performance of our machine learning model here. This part has significant relevance since it will allow us to understand the most important characteristics that led to our model development.
We will output the confusion matrix. It is a handy presentation of the accuracy of a model with two or more classes.
The table presents predictions on the x-axis and accuracy outcomes on the y-axis. The cells of the table are the number of predictions made by a machine learning algorithm.
According to an article the entries in the confusion matrix have the following meaning in the context of our study:
[[a b][c d]]
a is the number of correct predictions that an instance is negative,
b is the number of incorrect predictions that an instance is positive,
c is the number of incorrect of predictions that an instance is negative, and
d is the number of correct predictions that an instance is positive.
table(log.prediction.rd, test[,18])
log.prediction.rd 0 1
0 6832 1517
1 170 481
We’ll write a simple function to print the accuracy below
This tutorial has given you a brief and concise overview of the Logistic Regression algorithm and all the steps involved in achieving better results from our model. This notebook has also highlighted a few methods related to Exploratory Data Analysis, Pre-processing, and Evaluation, however, there are several other methods that we would encourage to explore on our blog or video tutorials.
If you want to take a deeper dive into several data science techniques. Join our 5-day hands-on Data Science Bootcamp preferred by working professionals, we cover the following topics:
Fundamentals of Data Mining
Machine Learning Fundamentals
Introduction to R
Introduction to Azure Machine Learning Studio
Data Exploration, Visualization, and Feature Engineering
Decision Tree Learning
Ensemble Methods: Bagging, Boosting, and Random Forest
