Learn how logistic regression fits a dataset to make predictions in R, as well as when and why to use it.
Logistic regression is one of the statistical techniques in machine learning used to form prediction models. It is one of the most popular classification algorithms mostly used for binary classification problems (problems with two class values, however, some variants may deal with multiple classes as well). It’s used for various research and industrial problems.
Therefore, it is essential to have a good grasp of logistic regression algorithms while learning data science. This tutorial is a sneak peek from many of Data Science Dojo’s hands-on exercises from their data science Bootcamp program, you will learn how logistic regression fits a dataset to make predictions, as well as when and why to use it.
In short, Logistic Regression is used when the dependent variable(target) is categorical. For example:
- To predict whether an email is spam (1) or not spam (0)
- Whether the tumor is malignant (1) or not (0)
Intro to Logistic Regression
It is named ‘Logistic Regression’ because its underlying technology is quite the same as Linear Regression. There are structural differences in how linear and logistic regression operate. Therefore, linear regression isn’t suitable to be used for classification problems. This link answers in detail why linear regression isn’t the right approach for classification.
Its name is derived from one of the core functions behind its implementation called the logistic function or the sigmoid function. It’s an S-shaped curve that can take any real-valued number and map it into a value between 0 and 1, but never exactly at those limits.
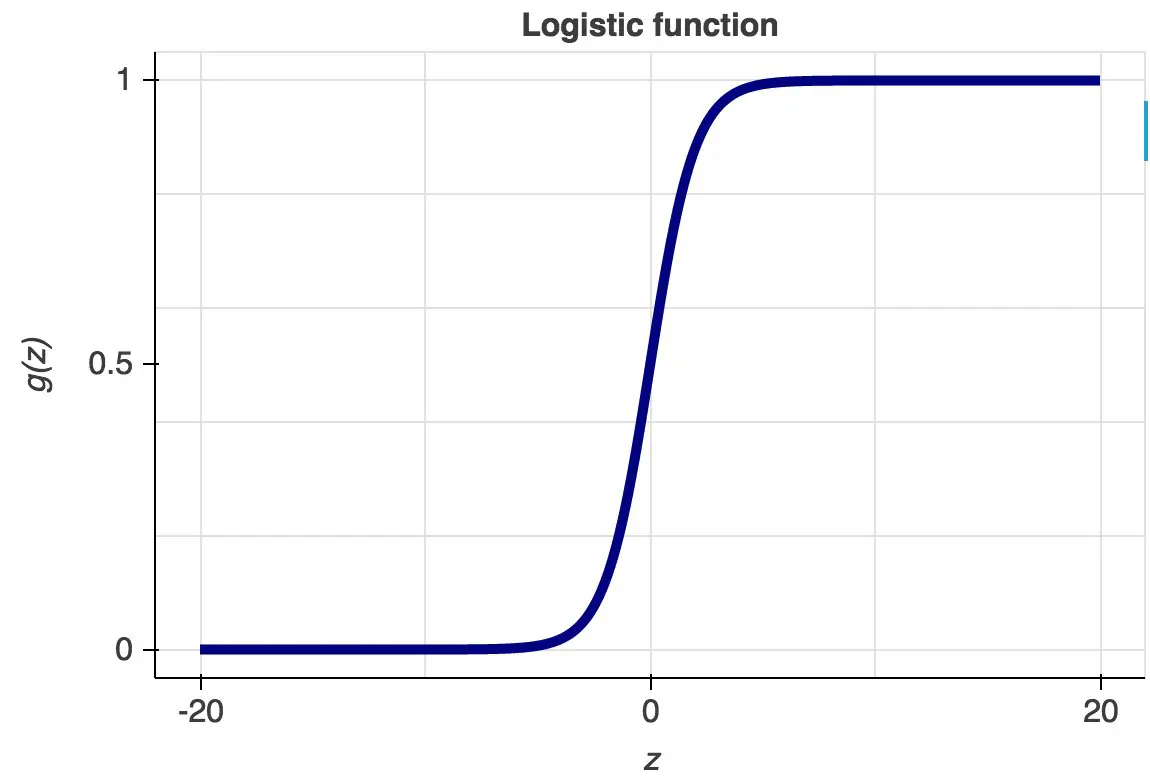
The hypothesis function of logistic regression can be seen below where the function g(z) is also shown.
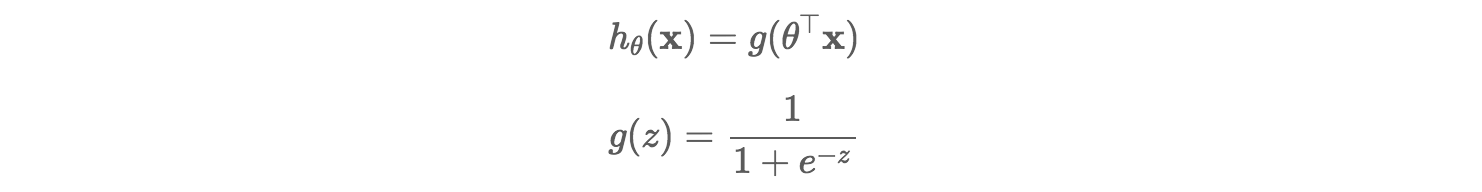
The hypothesis for logistic regression now becomes:
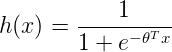
Here θ (theta) is a vector of parameters that our model will calculate to fit our classifier.
After calculations from the above equations, the cost function is now as follows:
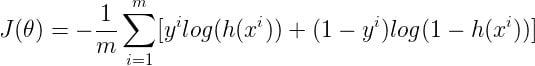
This tutorial will follow the format below to provide you with hands-on practice with Logistic Regression:
- Importing Libraries
- Importing Datasets
- Exploratory Data Analysis
- Feature Engineering
- Pre-processing
- Model Development
- Prediction
- Evaluation
The scenario
In this tutorial, we will be working with the Default of Credit Card Clients Data Set. This data set has 30000 rows and 24 columns. The data set could be used to estimate the probability of default payment by credit card clients using the data provided. These attributes are related to various details about a customer, his past payment information, and bill statements. It is hosted in Data Science Dojo’s repository.
Think of yourself as a lead data scientist employed at a large bank. You have been assigned to predict whether a particular customer will default on their payment next month or not. The result is an extremely valuable piece of information for the bank to make decisions regarding offering credit to its customers and could massively affect the bank’s revenue. Therefore, your task is very critical. You will learn to use logistic regression to solve this problem.
The dataset is a tricky one as it has a mix of categorical and continuous variables. Moreover, you will also get a chance to practice these concepts through short assignments given at the end of a few sub-modules. Feel free to change the parameters in the given methods once you have been through the entire notebook.
1) Importing libraries
We’ll begin by importing the dependencies that we require. The following dependencies are popularly used for data-wrangling operations and visualizations. We would encourage you to have a look at their documentation.
library(knitr)
library(tidyverse)
library(ggplot2)
library(mice)
library(lattice)
library(reshape2)
#install.packages("DataExplorer") if the following package is not available
library(DataExplorer)2) Importing Datasets
The dataset is available at Data Science Dojo’s repository in the following link. We’ll use the head method to view the first few rows.
## Need to fetch the excel file
path <- "https://code.datasciencedojo.com/datasciencedojo/datasets/raw/master/
Default%20of%20Credit%20Card%20Clients/default%20of%20credit%20card%20clients.csv"
data <- read.csv(file = path, header = TRUE)
head(data)

Since the header names are in the first row of the dataset, we’ll use the code below to first assign the headers to be the one from the first row and then delete the first row from the dataset. This way we will get our desired form.
colnames(data) <- as.character(unlist(data[1,]))
data = data[-1, ]
head(data)To avoid any complications ahead, we’ll rename our target variable “default payment next month” to a name without spaces using the code below.
colnames(data)[colnames(data)=="default payment next month"] <- "default_payment"
head(data)3) Exploratory data analysis
Data Exploration is one of the most significant portions of the machine-learning process. Clean data can ensure a notable increase in the accuracy of our model. No matter how powerful our model is, it cannot function well unless the data we provide has been thoroughly processed.
This step will briefly take you through this step and assist you in visualizing your data, finding the relation between variables, dealing with missing values and outliers, and assisting in getting some fundamental understanding of each variable we’ll use.
Moreover, this step will also enable us to figure out the most important attributes to feed our model and discard those that have no relevance.
We will start by using the dim function to print out the dimensionality of our data frame.
dim(data)30000 25
The str method will allow us to know the data type of each variable. We’ll transform it to a numeric data type since it’ll be easier to use for our functions ahead.
str(data)'data.frame': 30000 obs. of 25 variables: $ ID : Factor w/ 30001 levels "1","10","100",..: 1 11112 22223 23335 24446 25557 26668 27779 28890 2 ... $ LIMIT_BAL : Factor w/ 82 levels "10000","100000",..: 14 5 81 48 48 48 49 2 7 14 ... $ SEX : Factor w/ 3 levels "1","2","SEX": 2 2 2 2 1 1 1 2 2 1 ... $ EDUCATION : Factor w/ 8 levels "0","1","2","3",..: 3 3 3 3 3 2 2 3 4 4 ... $ MARRIAGE : Factor w/ 5 levels "0","1","2","3",..: 2 3 3 2 2 3 3 3 2 3 ... $ AGE : Factor w/ 57 levels "21","22","23",..: 4 6 14 17 37 17 9 3 8 15 ... $ PAY_0 : Factor w/ 12 levels "-1","-2","0",..: 5 1 3 3 1 3 3 3 3 2 ... $ PAY_2 : Factor w/ 12 levels "-1","-2","0",..: 5 5 3 3 3 3 3 1 3 2 ... $ PAY_3 : Factor w/ 12 levels "-1","-2","0",..: 1 3 3 3 1 3 3 1 5 2 ... $ PAY_4 : Factor w/ 12 levels "-1","-2","0",..: 1 3 3 3 3 3 3 3 3 2 ... $ PAY_5 : Factor w/ 11 levels "-1","-2","0",..: 2 3 3 3 3 3 3 3 3 1 ... $ PAY_6 : Factor w/ 11 levels "-1","-2","0",..: 2 4 3 3 3 3 3 1 3 1 ... $ BILL_AMT1 : Factor w/ 22724 levels "-1","-10","-100",..: 13345 10030 10924 15026 21268 18423 12835 1993 1518 307 ... $ BILL_AMT2 : Factor w/ 22347 levels "-1","-10","-100",..: 11404 5552 3482 15171 16961 17010 13627 12949 3530 348 ... $ BILL_AMT3 : Factor w/ 22027 levels "-1","-10","-100",..: 18440 9759 3105 15397 12421 16866 14184 17258 2072 365 ... $ BILL_AMT4 : Factor w/ 21549 levels "-1","-10","-100",..: 378 11833 3620 10318 7717 6809 16081 8147 2129 378 ... $ BILL_AMT5 : Factor w/ 21011 levels "-1","-10","-100",..: 385 11971 3950 10407 6477 6841 14580 76 1796 2638 ... $ BILL_AMT6 : Factor w/ 20605 levels "-1","-10","-100",..: 415 11339 4234 10458 6345 7002 14057 15748 12215 3230 ... $ PAY_AMT1 : Factor w/ 7944 levels "0","1","10","100",..: 1 1 1495 2416 2416 3160 5871 4578 4128 1 ... $ PAY_AMT2 : Factor w/ 7900 levels "0","1","10","100",..: 6671 5 1477 2536 4508 2142 4778 6189 1 1 ... $ PAY_AMT3 : Factor w/ 7519 levels "0","1","10","100",..: 1 5 5 646 6 6163 4292 1 4731 1 ... $ PAY_AMT4 : Factor w/ 6938 levels "0","1","10","100",..: 1 5 5 337 6620 5 2077 5286 5 813 ... $ PAY_AMT5 : Factor w/ 6898 levels "0","1","10","100",..: 1 1 5 263 5777 5 950 1502 5 408 ... $ PAY_AMT6 : Factor w/ 6940 levels "0","1","10","100",..: 1 2003 4751 5 5796 6293 963 1267 5 1 ... $ default_payment: Factor w/ 3 levels "0","1","default payment next month": 2 2 1 1 1 1 1 1 1 1 ...
data[, 1:25] <- sapply(data[, 1:25], as.character)We have involved an intermediate step by converting our data to character first. We need to use as.character before as.numeric. This is because factors are stored internally as integers with a table to give the factor level labels. Just using as.numeric will only give the internal integer codes.
data[, 1:25] <- sapply(data[, 1:25], as.numeric)
str(data)'data.frame': 30000 obs. of 25 variables: $ ID : num 1 2 3 4 5 6 7 8 9 10 ... $ LIMIT_BAL : num 20000 120000 90000 50000 50000 50000 500000 100000 140000 20000 ... $ SEX : num 2 2 2 2 1 1 1 2 2 1 ... $ EDUCATION : num 2 2 2 2 2 1 1 2 3 3 ... $ MARRIAGE : num 1 2 2 1 1 2 2 2 1 2 ... $ AGE : num 24 26 34 37 57 37 29 23 28 35 ... $ PAY_0 : num 2 -1 0 0 -1 0 0 0 0 -2 ... $ PAY_2 : num 2 2 0 0 0 0 0 -1 0 -2 ... $ PAY_3 : num -1 0 0 0 -1 0 0 -1 2 -2 ... $ PAY_4 : num -1 0 0 0 0 0 0 0 0 -2 ... $ PAY_5 : num -2 0 0 0 0 0 0 0 0 -1 ... $ PAY_6 : num -2 2 0 0 0 0 0 -1 0 -1 ... $ BILL_AMT1 : num 3913 2682 29239 46990 8617 ... $ BILL_AMT2 : num 3102 1725 14027 48233 5670 ... $ BILL_AMT3 : num 689 2682 13559 49291 35835 ... $ BILL_AMT4 : num 0 3272 14331 28314 20940 ... $ BILL_AMT5 : num 0 3455 14948 28959 19146 .. $ BILL_AMT6 : num 0 3261 15549 29547 19131 ... $ PAY_AMT1 : num 0 0 1518 2000 2000 ... $ PAY_AMT2 : num 689 1000 1500 2019 36681 ... $ PAY_AMT3 : num 0 1000 1000 1200 10000 657 38000 0 432 0 ... $ PAY_AMT4 : num 0 1000 1000 1100 9000 ... $ PAY_AMT5 : num 0 0 1000 1069 689 ... $ PAY_AMT6 : num 0 2000 5000 1000 679 ... $ default_payment: num 1 1 0 0 0 0 0 0 0 0 ...
When applied to a data frame, the summary() function is essentially applied to each column, and the results for all columns are shown together. For a continuous (numeric) variable like “age”, it returns the 5-number summary showing 5 descriptive statistics as these are numeric values.
summary(data)
ID LIMIT_BAL SEX EDUCATION
Min. : 1 Min. : 10000 Min. :1.000 Min. :0.000
1st Qu.: 7501 1st Qu.: 50000 1st Qu.:1.000 1st Qu.:1.000
Median :15000 Median : 140000 Median :2.000 Median :2.000
Mean :15000 Mean : 167484 Mean :1.604 Mean :1.853
3rd Qu.:22500 3rd Qu.: 240000 3rd Qu.:2.000 3rd Qu.:2.000
Max. :30000 Max. :1000000 Max. :2.000 Max. :6.000
MARRIAGE AGE PAY_0 PAY_2
Min. :0.000 Min. :21.00 Min. :-2.0000 Min. :-2.0000
1st Qu.:1.000 1st Qu.:28.00 1st Qu.:-1.0000 1st Qu.:-1.0000
Median :2.000 Median :34.00 Median : 0.0000 Median : 0.0000
Mean :1.552 Mean :35.49 Mean :-0.0167 Mean :-0.1338
3rd Qu.:2.000 3rd Qu.:41.00 3rd Qu.: 0.0000 3rd Qu.: 0.0000
Max. :3.000 Max. :79.00 Max. : 8.0000 Max. : 8.0000
PAY_3 PAY_4 PAY_5 PAY_6
Min. :-2.0000 Min. :-2.0000 Min. :-2.0000 Min. :-2.0000
1st Qu.:-1.0000 1st Qu.:-1.0000 1st Qu.:-1.0000 1st Qu.:-1.0000
Median : 0.0000 Median : 0.0000 Median : 0.0000 Median : 0.0000
Mean :-0.1662 Mean :-0.2207 Mean :-0.2662 Mean :-0.2911
3rd Qu.: 0.0000 3rd Qu.: 0.0000 3rd Qu.: 0.0000 3rd Qu.: 0.0000
Max. : 8.0000 Max. : 8.0000 Max. : 8.0000 Max. : 8.0000
BILL_AMT1 BILL_AMT2 BILL_AMT3 BILL_AMT4
Min. :-165580 Min. :-69777 Min. :-157264 Min. :-170000
1st Qu.: 3559 1st Qu.: 2985 1st Qu.: 2666 1st Qu.: 2327
Median : 22382 Median : 21200 Median : 20089 Median : 19052
Mean : 51223 Mean : 49179 Mean : 47013 Mean : 43263
3rd Qu.: 67091 3rd Qu.: 64006 3rd Qu.: 60165 3rd Qu.: 54506
Max. : 964511 Max. :983931 Max. :1664089 Max. : 891586
BILL_AMT5 BILL_AMT6 PAY_AMT1 PAY_AMT2
Min. :-81334 Min. :-339603 Min. : 0 Min. : 0
1st Qu.: 1763 1st Qu.: 1256 1st Qu.: 1000 1st Qu.: 833
Median : 18105 Median : 17071 Median : 2100 Median : 2009
Mean : 40311 Mean : 38872 Mean : 5664 Mean : 5921
3rd Qu.: 50191 3rd Qu.: 49198 3rd Qu.: 5006 3rd Qu.: 5000
Max. :927171 Max. : 961664 Max. :873552 Max. :1684259
PAY_AMT3 PAY_AMT4 PAY_AMT5 PAY_AMT6
Min. : 0 Min. : 0 Min. : 0.0 Min. : 0.0
1st Qu.: 390 1st Qu.: 296 1st Qu.: 252.5 1st Qu.: 117.8
Median : 1800 Median : 1500 Median : 1500.0 Median : 1500.0
Mean : 5226 Mean : 4826 Mean : 4799.4 Mean : 5215.5
3rd Qu.: 4505 3rd Qu.: 4013 3rd Qu.: 4031.5 3rd Qu.: 4000.0
Max. :896040 Max. :621000 Max. :426529.0 Max. :528666.0
default_payment
Min. :0.0000
1st Qu.:0.0000
Median :0.0000
Mean :0.2212
3rd Qu.:0.0000
Max. :1.0000
Using the introduced method, we can get to know the basic information about the dataframe, including the number of missing values in each variable.
introduce(data)As we can observe, there are no missing values in the dataframe.
The information in summary above gives a sense of the continuous and categorical features in our dataset. However, evaluating these details against the data description shows that categorical values such as EDUCATION and MARRIAGE have categories beyond those given in the data dictionary. We’ll find out these extra categories using the value_counts method.
count(data, vars = EDUCATION)
| vars | n |
|---|---|
| 0 | 14 |
| 1 | 10585 |
| 2 | 14030 |
| 3 | 4917 |
| 4 | 123 |
| 5 | 280 |
| 6 | 51 |
The data dictionary defines the following categories for EDUCATION: “Education (1 = graduate school; 2 = university; 3 = high school; 4 = others)”. However, we can also observe 0 along with numbers greater than 4, i.e. 5 and 6. Since we don’t have any further details about it, we can assume 0 to be someone with no educational experience and 0 along with 5 & 6 can be placed in others along with 4.
count(data, vars = MARRIAGE)
| vars | n |
|---|---|
| 0 | 54 |
| 1 | 13659 |
| 2 | 15964 |
| 3 | 323 |
The data dictionary defines the following categories for MARRIAGE: “Marital status (1 = married; 2 = single; 3 = others)”. Since category 0 hasn’t been defined anywhere in the data dictionary, we can include it in the ‘others’ category marked as 3.
#replace 0's with NAN, replace others too
data$EDUCATION[data$EDUCATION == 0] <- 4
data$EDUCATION[data$EDUCATION == 5] <- 4
data$EDUCATION[data$EDUCATION == 6] <- 4
data$MARRIAGE[data$MARRIAGE == 0] <- 3count(data, vars = MARRIAGE)
count(data, vars = EDUCATION)
| vars | n |
|---|---|
| 1 | 13659 |
| 2 | 15964 |
| 3 | 377 |
| vars | n |
|---|---|
| 1 | 10585 |
| 2 | 14030 |
| 3 | 4917 |
| 4 | 468 |
We’ll now move on to a multi-variate analysis of our variables and draw a correlation heat map from the DataExplorer library. The heatmap will enable us to find out the correlation between each variable. We are more interested in finding out the correlation between our predictor attributes with the target attribute default payment next month. The color scheme depicts the strength of the correlation between the 2 variables.
This will be a simple way to quickly find out how much of an impact a variable has on our final outcome. There are other ways as well to figure this out.
plot_correlation(na.omit(data), maxcat = 5L)
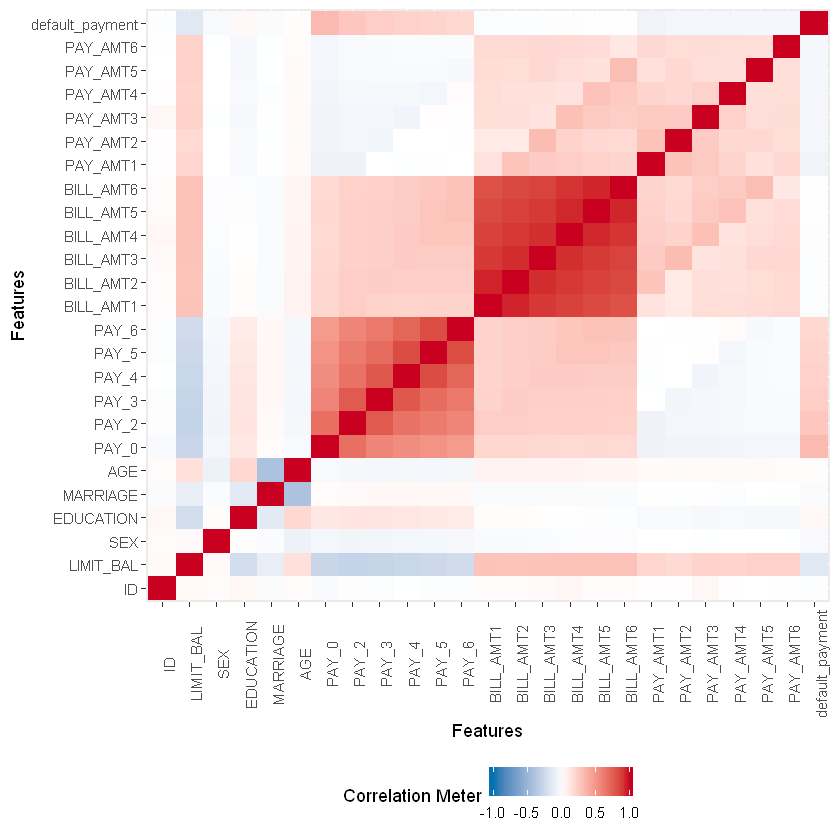
We can observe the weak correlation of AGE, BILL_AMT1, BILL_AMT2, BILL_AMT3, BILL_AMT4, BILL_AMT5, and BILL_AMT6 with our target variable.
Now let’s have a univariate analysis of our variables. We’ll start with the categorical variables and have a quick check on the frequency of distribution of categories. The code below will allow us to observe the required graphs. We’ll first draw the distribution for all PAY variables.
plot_histogram(data)
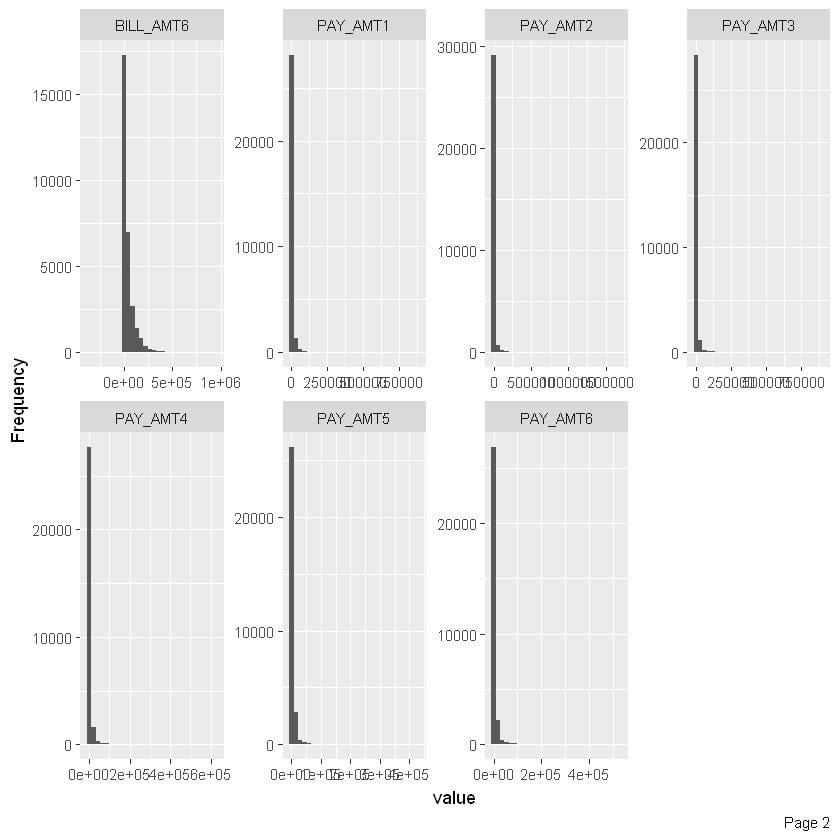
We can make a few observations from the above histogram. The distribution above shows that nearly all PAY attributes are rightly skewed.
4) Feature engineering
This step can be more important than the actual model used because a machine learning algorithm only learns from the data we give it, and creating features that are relevant to a task is absolutely crucial.
Analyzing our data above, we’ve been able to note the extremely weak correlation of some variables with the final target variable. The following are the ones that have significantly low correlation values: AGE, BILL_AMT2, BILL_AMT3, BILL_AMT4, BILL_AMT5, BILL_AMT6.
#deleting columns
data_new <- select(data, -one_of('ID','AGE', 'BILL_AMT2',
'BILL_AMT3','BILL_AMT4','BILL_AMT5','BILL_AMT6'))
head(data_new)

5) Pre-processing
Standardization is a transformation that centers the data by removing the mean value of each feature and then scaling it by dividing (non-constant) features by their standard deviation. After standardizing data the mean will be zero and the standard deviation one.
It is most suitable for techniques that assume a Gaussian distribution in the input variables and work better with rescaled data, such as linear regression, logistic regression, and linear discriminate analysis. If a feature has a variance that is orders of magnitude larger than others, it might dominate the objective function and make the estimator unable to learn from other features correctly as expected.
In the code below, we’ll use the scale method to transform our dataset using it.
data_new[, 1:17] <- scale(data_new[, 1:17])
head(data_new)

The next task we’ll do is to split the data for training and testing as we’ll use our test data to evaluate our model. We will now split our dataset into train and test. We’ll change it to 0.3. Therefore, 30% of the dataset is reserved for testing while the remaining is for training. By default, the dataset will also be shuffled before splitting.
#create a list of random number ranging from 1 to number of rows from actual data
#and 70% of the data into training data
data2 = sort(sample(nrow(data_new), nrow(data_new)*.7))
#creating training data set by selecting the output row values
train <- data_new[data2,]
#creating test data set by not selecting the output row values
test <- data_new[-data2,]
Let us print the dimensions of all these variables using the dim method. You can notice the 70-30% split.
dim(train)
dim(test)
21000 18
9000 18
6) Model development
We will now move on to the most important step of developing our logistic regression model. We have already fetched our machine learning model in the beginning. Now with a few lines of code, we’ll first create a logistic regression model which has been imported from sci-kit learn’s linear model package to our variable named model.
Following this, we’ll train our model using the fit method with X_train and y_train which contain 70% of our dataset. This will be a binary classification model.
## fit a logistic regression model with the training dataset
log.model <- glm(default_payment ~., data = train, family = binomial(link = "logit"))
summary(log.model)
Call:
glm(formula = default_payment ~ ., family = binomial(link = "logit"),
data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.1171 -0.6998 -0.5473 -0.2946 3.4915
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.465097 0.019825 -73.900 < 2e-16 ***
LIMIT_BAL -0.083475 0.023905 -3.492 0.000480 ***
SEX -0.082986 0.017717 -4.684 2.81e-06 ***
EDUCATION -0.059851 0.019178 -3.121 0.001803 **
MARRIAGE -0.107322 0.018350 -5.849 4.95e-09 ***
PAY_0 0.661918 0.023605 28.041 < 2e-16 ***
PAY_2 0.069704 0.028842 2.417 0.015660 *
PAY_3 0.090691 0.031982 2.836 0.004573 **
PAY_4 0.074336 0.034612 2.148 0.031738 *
PAY_5 0.018469 0.036430 0.507 0.612178
PAY_6 0.006314 0.030235 0.209 0.834584
BILL_AMT1 -0.123582 0.023558 -5.246 1.56e-07 ***
PAY_AMT1 -0.136745 0.037549 -3.642 0.000271 ***
PAY_AMT2 -0.246634 0.056432 -4.370 1.24e-05 ***
PAY_AMT3 -0.014662 0.028012 -0.523 0.600677
PAY_AMT4 -0.087782 0.031484 -2.788 0.005300 **
PAY_AMT5 -0.084533 0.030917 -2.734 0.006254 **
PAY_AMT6 -0.027355 0.025707 -1.064 0.287277
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 22176 on 20999 degrees of freedom
Residual deviance: 19535 on 20982 degrees of freedom
AIC: 19571
Number of Fisher Scoring iterations: 6
7) Prediction
Below we’ll use the prediction method to find out the predictions made by our Logistic Regression method. We will first store the predicted results in our y_pred variable and print the first 10 rows of our test data set. Following this we will print the predicted values of the corresponding rows and the original labels that were stored in y_test for comparison.
test[1:10,]

## to predict using logistic regression model, probablilities obtained
log.predictions <- predict(log.model, test, type="response")
## Look at probability output
head(log.predictions, 10)
- 2
- 0.539623162720197
- 7
- 0.232835137994762
- 10
- 0.25988780274953
- 11
- 0.0556716133560243
- 15
- 0.422481223473459
- 22
- 0.165384552048511
- 25
- 0.0494775267027534
- 26
- 0.238225423596718
- 31
- 0.248366972046479
- 37
- 0.111907725985513
Below we are going to assign our labels with the decision rule that if the prediction is greater than 0.5, assign it 1 else 0.
log.prediction.rd <- ifelse(log.predictions > 0.5, 1, 0)
head(log.prediction.rd, 10)
- 2
- 1
- 7
- 0
- 10
- 0
- 11
- 0
- 15
- 0
- 22
- 0
- 25
- 0
- 26
- 0
- 31
- 0
- 37
- 0
Evaluation
We’ll now discuss a few evaluation metrics to measure the performance of our machine-learning model here. This part has significant relevance since it will allow us to understand the most important characteristics that led to our model development.
We will output the confusion matrix. It is a handy presentation of the accuracy of a model with two or more classes.
The table presents predictions on the x-axis and accuracy outcomes on the y-axis. The cells of the table are the number of predictions made by a machine learning algorithm.
According to an article the entries in the confusion matrix have the following meaning in the context of our study:
[[a b][c d]]
- a is the number of correct predictions that an instance is negative,
- b is the number of incorrect predictions that an instance is positive,
- c is the number of incorrect predictions that an instance is negative, and
- d is the number of correct predictions that an instance is positive.
table(log.prediction.rd, test[,18])
log.prediction.rd 0 1
0 6832 1517
1 170 481
We’ll write a simple function to print the accuracy below
accuracy <- table(log.prediction.rd, test[,18])
sum(diag(accuracy))/sum(accuracy)
0.812555555555556
Conclusion
This tutorial has given you a brief and concise overview of the Logistic Regression algorithm and all the steps involved in achieving better results from our model. This notebook has also highlighted a few methods related to Exploratory Data Analysis, Pre-processing, and Evaluation, however, there are several other methods that we would encourage you to explore on our blog or video tutorials.
If you want to take a deeper dive into several data science techniques. Join our 5-day hands-on Data Science Bootcamp preferred by working professionals, we cover the following topics:
- Fundamentals of Data Mining
- Machine Learning Fundamentals
- Introduction to R
- Introduction to Azure Machine Learning Studio
- Data Exploration, Visualization, and Feature Engineering
- Decision Tree Learning
- Ensemble Methods: Bagging, Boosting, and Random Forest
- Regression: Cost Functions, Gradient Descent, Regularization
- Unsupervised Learning
- Recommendation Systems
- Metrics and Methods for Evaluating Predictive Models
- Introduction to Online Experimentation and A/B Testing
- Fundamentals of Big Data Engineering
- Hadoop and Hive
- Message Queues and Real-time Analytics
- NoSQL Databases and HBase
- Hack Project: Creating a Real-time IoT Pipeline
- Naive Bayes
- Logistic Regression
- Times Series Forecasting
This post was originally sponsored on What’s The Big Data.




