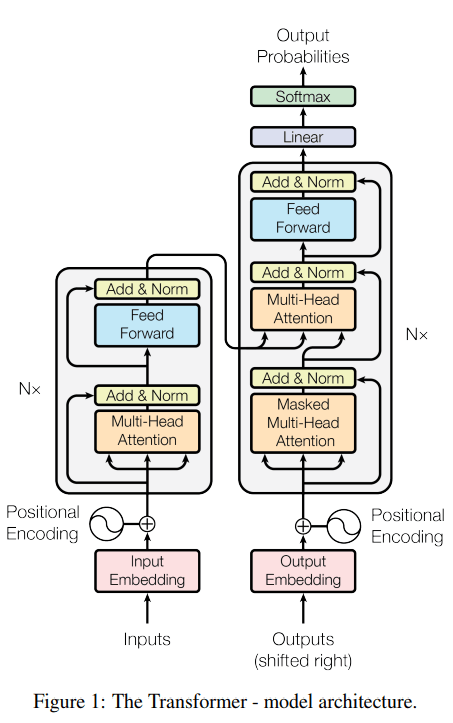
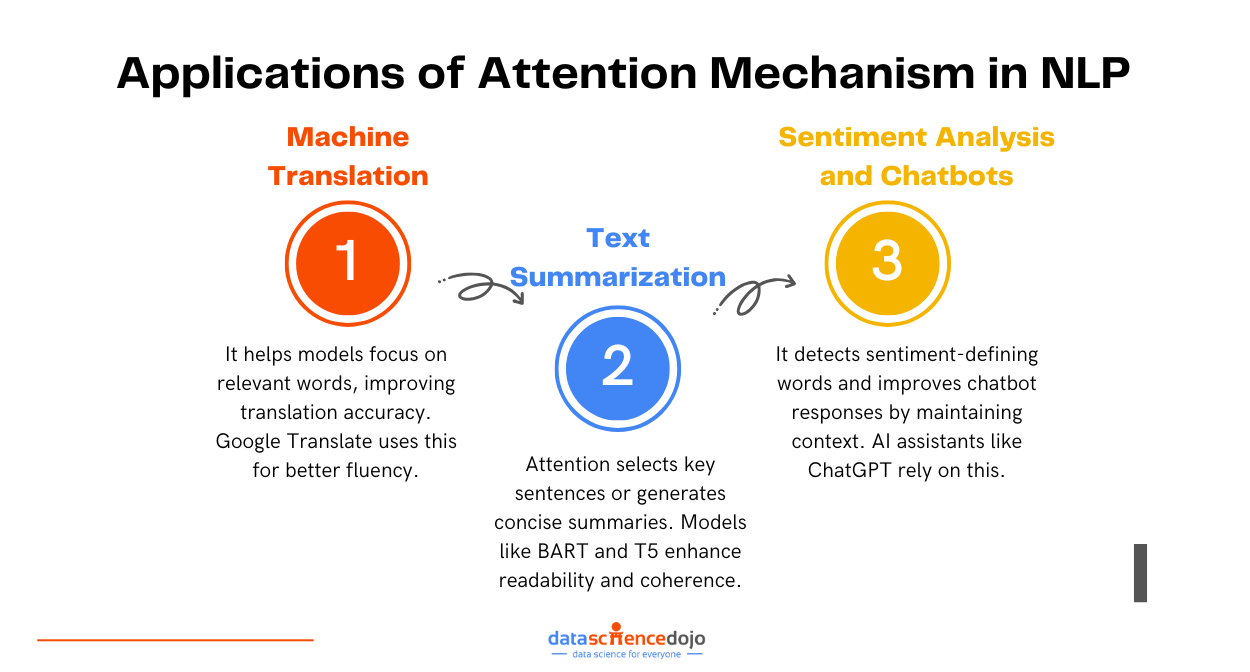
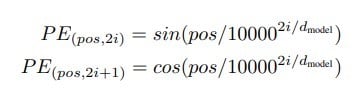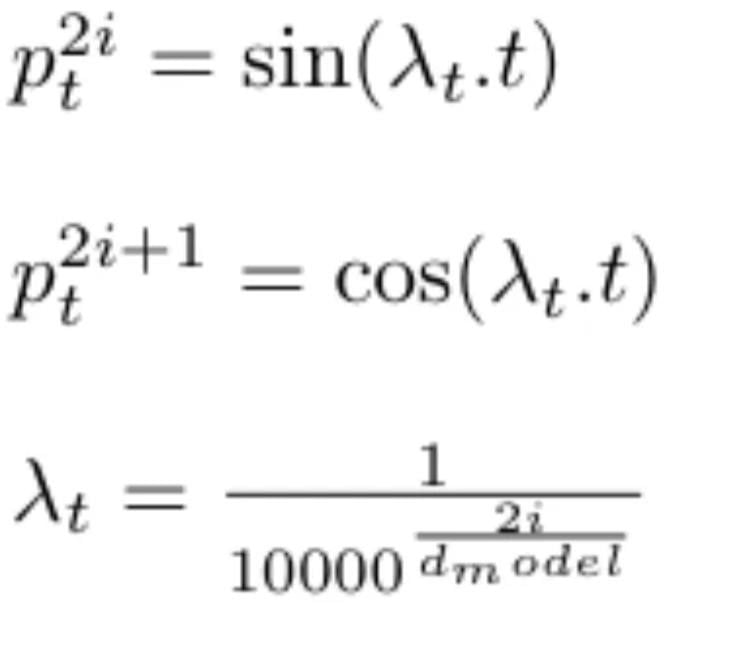Data is a crucial element of modern-day businesses. With the growing use of machine learning (ML) models to handle, store, and manage data, the efficiency and impact of enterprises have also increased. It has led to advanced techniques for data management, where each tactic is based on the type of data and the way to handle it.
Learn more about revolutionizing Enterprise Data Management
Categorical data is one such form of information that is handled by ML models using different methods. In this blog, we will explore the basics of categorical data. We will also explore the 7 main encoding methods used to process categorical data.
What is Categorical Data?
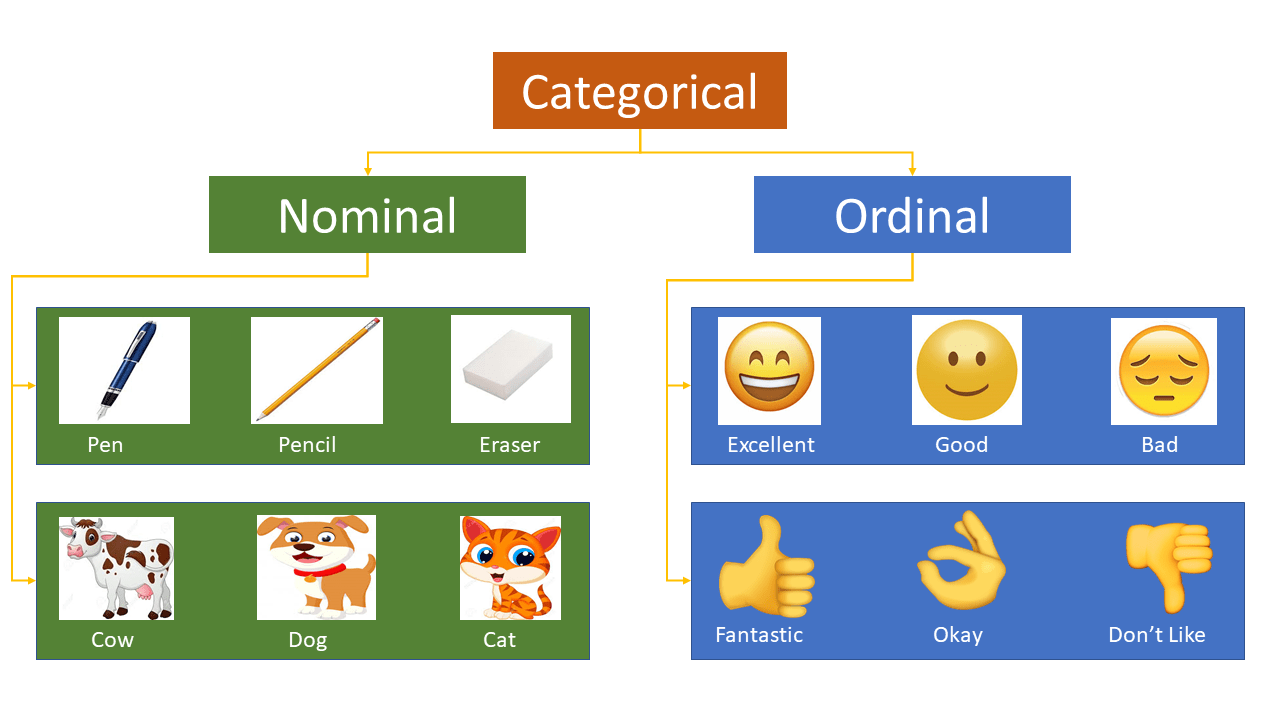
Categorical data, also known as nominal or ordinal data, consists of values that fall into distinct categories or groups. Unlike numerical data, which represents measurable quantities, categorical data represents qualitative or descriptive characteristics. These variables can be represented as strings or labels and have a finite number of possible values.
Examples of Categorical Data
- Nominal Data: Categories that do not have an inherent order or ranking. For instance, the city where a person lives (e.g., Delhi, Mumbai, Ahmedabad, Bangalore).
- Ordinal Data: Categories that have an inherent order or ranking. For example, the highest degree a person has (e.g., High School, Diploma, Bachelor’s, Master’s, Ph.D.).
Importance of Categorical Data in Machine Learning
Categorical data is crucial in machine learning for several reasons. ML models often require numerical input, so categorical data must be converted into a numerical format for effective processing and analysis. Here are some key points highlighting the importance of categorical data in machine learning:
Explore machine learning roadmap
1. Model Compatibility
Most machine learning algorithms work with numerical data, making it essential to transform categorical variables into numerical values. This conversion allows models to process the data and extract valuable information.
2. Pattern Recognition
Encoding categorical data helps models identify patterns within the data. For instance, specific categories might be strongly associated with particular outcomes, and recognizing these patterns can improve model accuracy and predictive power.
Understand Design Patterns for AI Agents in LLMs
3. Bias Prevention
Proper encoding ensures that all features are equally weighted, preventing bias. For example, one-hot encoding and other methods help avoid unintended biases that might arise from the categorical nature of the data.
Explore 7 Essential Encoding Techniques for Categorical Data in Machine Learning
4. Feature Engineering
Encoding categorical data is a crucial part of feature engineering, which involves creating features that make ML models more effective. Effective feature engineering, including proper encoding, can significantly enhance model performance.
Learn about 101 ML algorithms for data science with cheat sheets
5. Handling High Cardinality
Advanced encoding techniques like target encoding and hashing are used to manage high cardinality features efficiently. These techniques help reduce dimensionality and computational complexity, making models more scalable and efficient.
6. Avoiding the Dummy Variable Trap
While techniques like one-hot encoding are popular, they can lead to issues like the dummy variable trap, where features become highly correlated. Understanding and addressing these issues through proper encoding methods is essential for robust model performance.
7. Improving Model Interpretability
Encoded categorical data can make models more interpretable. For example, target encoding provides a direct relationship between the categorical feature and the target variable, making it easier to understand how different categories influence the model’s predictions.
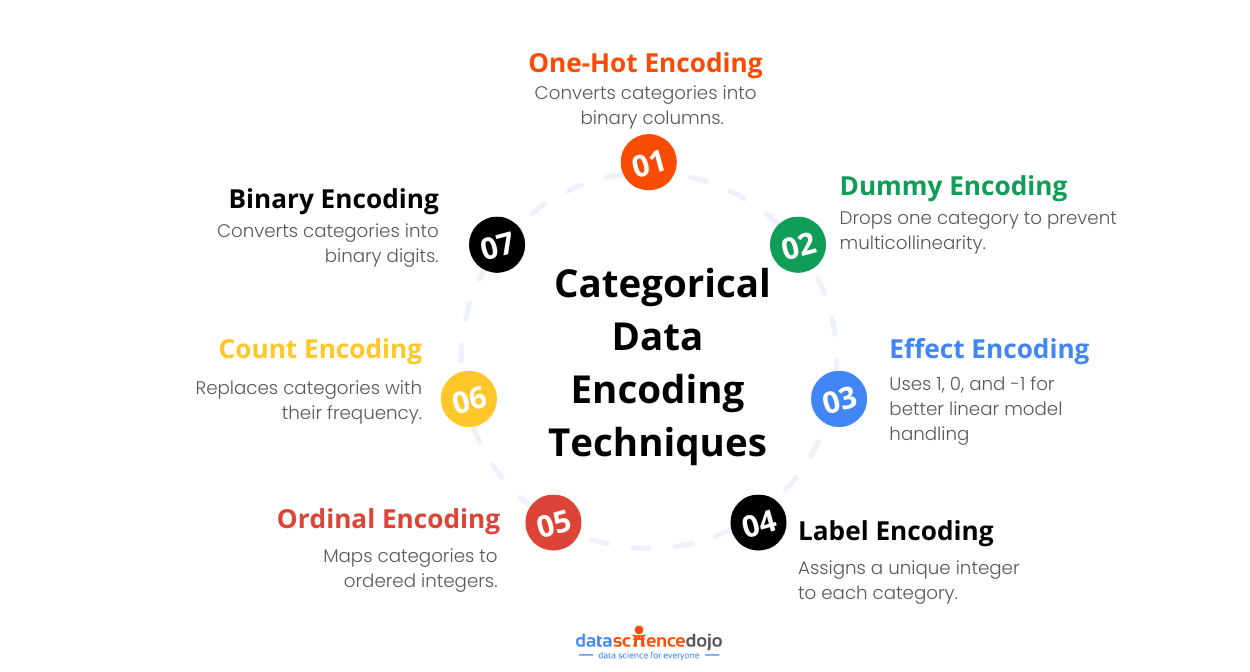
7 Encoding Techniques for Categorical Data
Let’s take a deeper look into 7 main encoding techniques for categorical data.
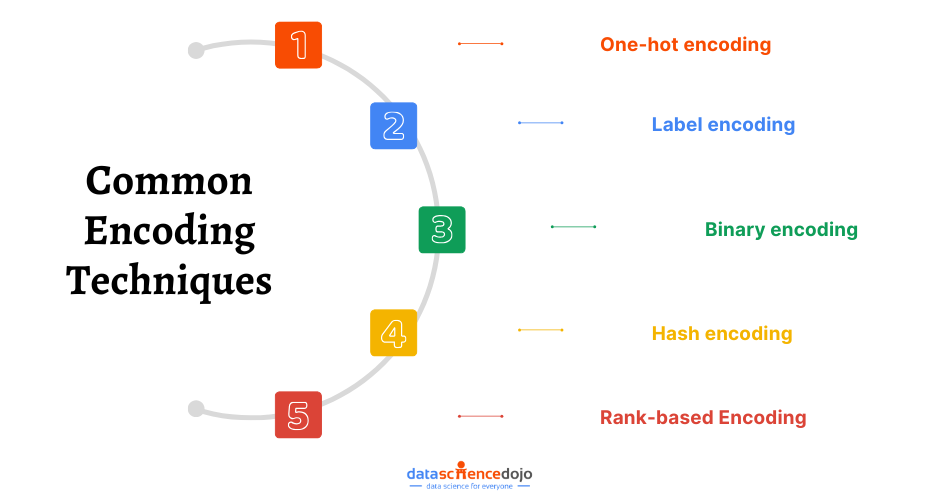
1. One-Hot Encoding
One-hot encoding, also known as dummy encoding, is a popular technique for converting categorical data into a numerical format. This technique is particularly suitable for nominal categorical features where the categories have no inherent order or ranking.
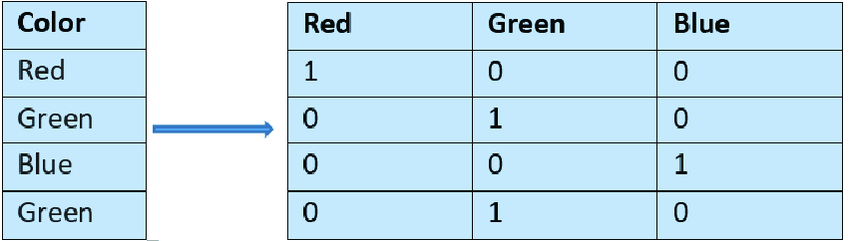
How One-Hot Encoding Works?
- Determine the categorical feature in your dataset that needs to be encoded.
- For each unique category in the feature, create a new binary column.
- Assign 1 to the column that corresponds to the category of the data point and 0 to all other new columns.
Advantages of One-Hot Encoding
- Preserves Information: Maintains the distinctiveness of labels without implying any ordinality.
- Compatibility: Provides a numerical representation of categorical data, making it suitable for many machine learning algorithms.
Use Cases
- Nominal Data: When dealing with nominal data where categories have no meaningful order. For example, in a dataset containing the feature “Type of Animal” with categories like “Dog”, “Cat”, and “Bird”, one-hot encoding is ideal because there is no inherent ranking among the animals 2.
- Machine Learning Models: Particularly beneficial for algorithms that cannot handle categorical data directly, such as linear regression, logistic regression, and neural networks.
- Handling Missing Values: One-hot encoding handles missing values efficiently. If a category is absent, it results in all zeros in the one-hot encoded columns, which can be useful for certain ML models.
Challenges with One-Hot Encoding
- Curse of Dimensionality: It can lead to a high number of new columns (dimensions) in your dataset, increasing computational complexity and storage requirements.
- Multicollinearity: The newly created binary columns can be correlated, which can be problematic for some models that assume independence between features.
- Data Sparsity: One-hot encoding can result in sparse matrices where most entries are zeros, which can be memory-inefficient and affect model performance.
Hence, one-hot encoding is a powerful and widely used technique for converting categorical data into a numerical format, especially for nominal data. Understanding when and how to use one-hot encoding is crucial for effective feature engineering in machine learning projects.
2. Dummy Encoding
Dummy encoding is a technique for converting categorical variables into a numerical format by transforming them into a set of binary variables.
It is similar to one-hot encoding but with a key distinction: dummy encoding uses (N-1) binary variables to represent (N) categories, which helps to avoid multicollinearity issues commonly known as the dummy variable trap.

How Dummy Encoding Works?
Dummy encoding transforms each category in a categorical feature into a binary column, but it drops one category. The process can be explained as follows:
- Determine the categorical feature in your dataset that needs to be encoded.
- For each unique category in the feature (except one), create a new binary column.
- Assign 1 to the column that corresponds to the category of the data point and 0 to all other new columns.
Advantages of Dummy Encoding
- Avoids Multicollinearity: By dropping one category, dummy encoding prevents the dummy variable trap where one column can be perfectly predicted from the others.
- Preserves Information: Maintains the distinctiveness of labels without implying any ordinality.
Use Cases
Regression Models: Suitable for regression models where multicollinearity can be a significant issue. By using (N-1) binary variables for (N) categories, dummy encoding helps to avoid this problem.
Understand linear regression vs logistic regression
Nominal Data: When dealing with nominal data where categories have no meaningful order, dummy encoding is ideal. For example, in a dataset containing the feature “Department” with categories like “Finance”, “HR”, and “IT”, dummy encoding can be used to convert these categories into binary columns.
Challenges with Dummy Encoding
- Curse of Dimensionality: Similar to one-hot encoding, dummy encoding can lead to a high number of new columns (dimensions) in your dataset, increasing computational complexity and storage requirements.
- Data Sparsity: Dummy encoding can result in sparse matrices where most entries are zeros, which can be memory-inefficient and affect model performance.
However, dummy encoding is a useful technique for encoding categorical data. You must carefully choose this technique based on the details of your ML project.
Also, read about rank-based encoding
3. Effect Encoding
Effect encoding, also known as Deviation Encoding or Sum Encoding, is an advanced categorical data encoding technique. It is similar to dummy encoding but with a key difference: instead of using binary values (0 and 1), effect encoding uses three values: 1, 0, and -1.
This encoding is particularly useful when dealing with categorical variables in linear models because it helps to handle the multicollinearity issue more effectively.
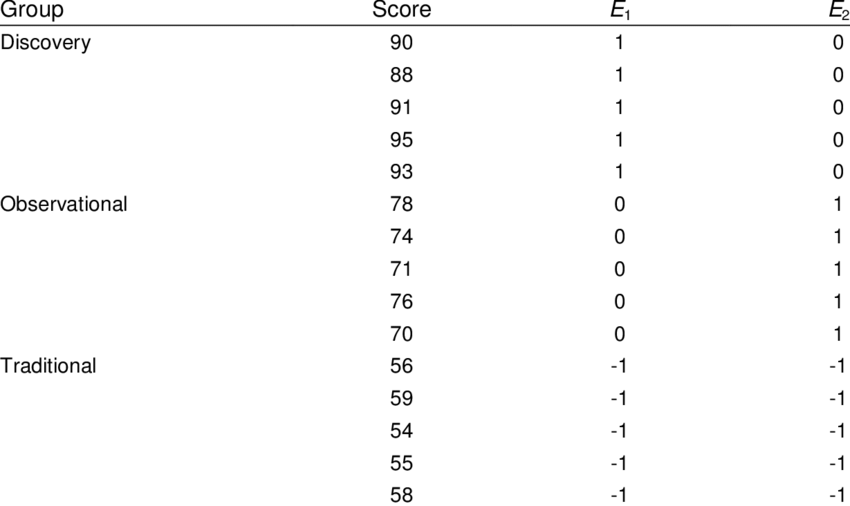
How does Effect Encoding Work?
In effect encoding, the categories of a feature are represented using 1, 0, and -1. The idea is to represent the absence of the first category (baseline category) by -1 in all corresponding binary columns.
- Determine the categorical feature in your dataset that needs to be encoded.
- For each unique category in the feature (except one), create a new binary column.
- Assign 1 to the column that corresponds to the category of the data point, 0 to all other new columns, and -1 to the row that would otherwise be all 0s in dummy encoding.
Advantages of Effect Encoding
- Avoids Multicollinearity: By using -1 in place of the baseline category, effect encoding helps to handle multicollinearity better than dummy encoding.
- Interpretable Coefficients: In linear models, the coefficients of effect-encoded variables are interpreted as deviations from the overall mean, which can sometimes make the model easier to interpret.
Use Cases
- Linear Models: When using linear regression or other linear models, effect encoding helps to handle multicollinearity issues effectively and makes the coefficients more interpretable.
- ANOVA (Analysis of Variance): Effect encoding is often used in ANOVA models for comparing group means.
Thus, effect encoding is an advanced technique for encoding categorical data, particularly beneficial for linear models due to its ability to handle multicollinearity and make coefficients interpretable.
4. Label Encoding
Label encoding is a technique used to convert categorical data into numerical data by assigning a unique integer to each category within a feature. This method is particularly useful for ordinal categorical features where the categories have a meaningful order or ranking.
By converting categories to numbers, label encoding makes categorical data compatible with machine learning algorithms that require numerical input.
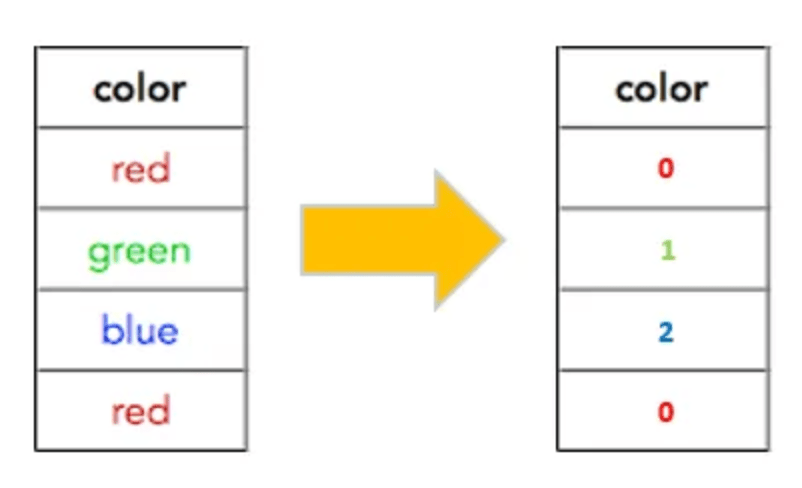
How Label Encoding Works?
Label encoding assigns a unique integer to each category in a feature. The integers are typically assigned in alphabetical order or based on their appearance in the data. For ordinal features, the integers represent the order of the categories.
- Determine the categorical feature in your dataset that needs to be encoded.
- Assign a unique integer to each category in the feature.
- Replace the original categories in the feature with their corresponding integer values.
Advantages of Label Encoding
- Simple and Efficient: It is straightforward and computationally efficient.
- Maintains Ordinality: It preserves the order of categories, which is essential for ordinal features.
Use Cases
- Ordinal Data: When dealing with ordinal features where the categories have a meaningful order. For example, education levels such as “High School”, “Bachelor’s Degree”, “Master’s Degree”, and “PhD” can be encoded as 0, 1, 2, and 3, respectively.
- Tree-Based Algorithms: Algorithms like decision trees and random forests can handle label-encoded data well because they can naturally work with the integer representation of categories.
Challenges with Label Encoding
- Unintended Ordinality: When used with nominal data (categories without a meaningful order), label encoding can introduce unintended ordinality, misleading the model to assume some form of ranking among the categories.
- Model Bias: Some machine learning algorithms might misinterpret the integer values as having a mathematical relationship, potentially leading to biased results.
Label encoding is a simple yet powerful technique for converting categorical data into numerical format, especially useful for ordinal features. However, it should be used with caution for nominal data to avoid introducing unintended relationships.
By following these guidelines and examples, you can effectively implement label encoding in your ML workflows to handle categorical data efficiently.
5. Ordinal Encoding
Ordinal encoding is a technique used to convert categorical data into numerical data by assigning a unique integer to each category within a feature, based on a meaningful order or ranking. This method is particularly useful for ordinal categorical features where the categories have a natural order.
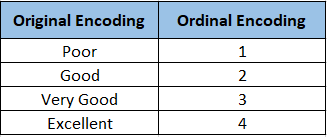
How Ordinal Encoding Works
Ordinal encoding involves mapping each category to a unique integer value that reflects the order of the categories. This method ensures that the encoded values preserve the inherent order among the categories. It can be summed into the following steps
- Determine the ordinal feature in your dataset that needs to be encoded.
- Establish a meaningful order for the categories.
- Assign a unique integer to each category based on their order.
- Replace the original categories in the feature with their corresponding integer values.
Advantages of Ordinal Encoding
- Preserves Order: It captures and preserves the ordinal relationships between categories, which can be valuable for certain types of analyses.
- Reduces Dimensionality: It reduces the dimensionality of the dataset compared to one-hot encoding, making it more memory-efficient.
- Compatible with Many Algorithms: It provides a numerical representation of the data, making it suitable for many machine learning algorithms.
Use Cases
- Ordinal Data: When dealing with categorical features that exhibit a clear and meaningful order or ranking. For example, education levels, satisfaction ratings, or any other feature with an inherent order.
- Machine Learning Models: Algorithms like linear regression, decision trees, and support vector machines can benefit from the ordered numerical representation of ordinal features.
Challenges with Ordinal Encoding
- Assumption of Linear Relationships: Some machine learning algorithms might assume a linear relationship between the encoded integers, which might not always be appropriate for all ordinal features.
- Not Suitable for Nominal Data: It should not be applied to nominal categorical features, where the categories do not have a meaningful order.
Ordinal encoding is especially useful for machine learning algorithms that need numerical input and can handle the ordered nature of the data.
6. Count Encoding
Count encoding, also known as frequency encoding, is a technique used to convert categorical features into numerical values based on the frequency of each category in the dataset.
This method assigns each category a numerical value representing how often it appears, thereby providing a straightforward numerical representation of the categories.
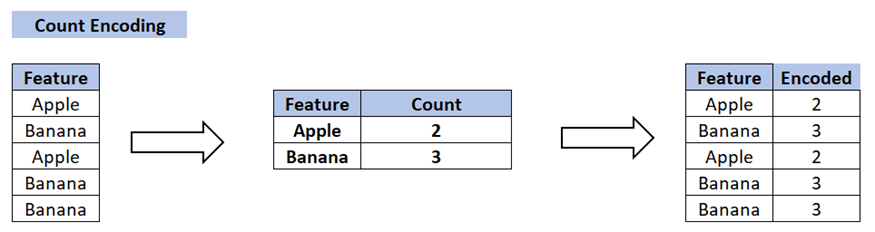
How Count Encoding Works
The process of count encoding involves mapping each category to its frequency or count within the dataset. Categories that appear more frequently receive higher values, while less common categories receive lower values. This can be particularly useful in scenarios where the frequency of categories carries significant information.
- Determine the categorical feature in your dataset that needs to be encoded.
- Calculate the frequency of each category within the feature.
- Assign the calculated frequencies as numerical values to each corresponding category.
- Replace the original categories in the feature with their corresponding frequency values.
Advantages of Count Encoding
- Simple and Interpretable: It provides a straightforward and interpretable way to encode categorical data, preserving the count information.
- Relevant for Frequency-Based Problems: Particularly useful when the frequency of categories is a relevant feature for the problem you’re solving.
- Reduces Dimensionality: It reduces the dimensionality compared to one-hot encoding, which can be beneficial in high-cardinality scenarios.
Use Cases
- Frequency-Relevant Features: When analyzing categorical features where the frequency of each category is relevant information for your model. For instance, in customer segmentation, the frequency of customer purchases might be crucial.
- High-Cardinality Features: When dealing with high-cardinality categorical features, where one-hot encoding would result in a large number of columns, count encoding provides a more compact representation.
Understand customer engagement through AI-powered marketing
Challenges with Count Encoding
- Loss of Category Information: It can lose some information about the distinctiveness of categories since categories with the same frequency will have the same encoded value.
- Not Suitable for Ordinal Data: It should not be applied to ordinal categorical features where the order of categories is important.
Count encoding is a valuable technique for scenarios where category frequencies carry significant information and when dealing with high-cardinality features.
7. Binary Encoding
Binary encoding is a versatile technique for encoding categorical features, especially when dealing with high-cardinality data. It combines the benefits of one-hot and label encoding while reducing dimensionality.
How Binary Encoding Works
Binary encoding involves converting each category into binary code and representing it as a sequence of binary digits (0s and 1s). Each binary digit is then placed in a separate column, effectively creating a set of binary columns for each category. The encoding process follows these steps:
- Assign a unique integer to each category, similar to label encoding.
- Convert the integer to binary code.
- Create a set of binary columns to represent the binary code.
Advantages of Binary Encoding
- Dimensionality Reduction: It reduces the dimensionality compared to one-hot encoding, especially for features with many unique categories.
- Memory Efficient: It is memory-efficient and overcomes the curse of dimensionality.
- Easy to Implement and Interpret: It is straightforward to implement and interpret.
Use Cases
- High-Cardinality Features: When dealing with high-cardinality categorical features (features with a large number of unique categories), binary encoding helps reduce the dimensionality of the dataset.
- Machine Learning Models: It is suitable for many machine learning algorithms that can handle binary input features effectively.
Challenges with Binary Encoding
- Complexity: Although binary encoding reduces dimensionality, it might still introduce complexity for features with extremely high cardinality.
- Handling Missing Values: Special care is needed to handle missing values during the encoding process.
Hence, binary encoding combines the advantages of one-hot encoding and label encoding, making it a suitable choice for many ML tasks.
Mastering Categorical Data Encoding for Enhanced Machine Learning
In summary, the effective handling of categorical data is a cornerstone of modern machine learning. With the growth of machine learning models, businesses can now manage data more efficiently, leading to improved enterprise performance.
Learn the top 9 machine learning algorithms to use for SEO & marketing
This blog has delved into the basics of categorical data and outlined seven critical encoding methods. Each method has its unique advantages, challenges, and specific use cases, making it essential to choose the right technique based on the nature of the data and the requirements of the model.
Proper encoding not only ensures compatibility with various models but also enhances pattern recognition, prevents bias, and improves feature engineering. By mastering these encoding techniques, data scientists can significantly improve model performance and make more informed predictions, ultimately driving better business outcomes.
You can also join our Discord community to stay posted and participate in discussions around machine learning, AI, LLMs, and much more!