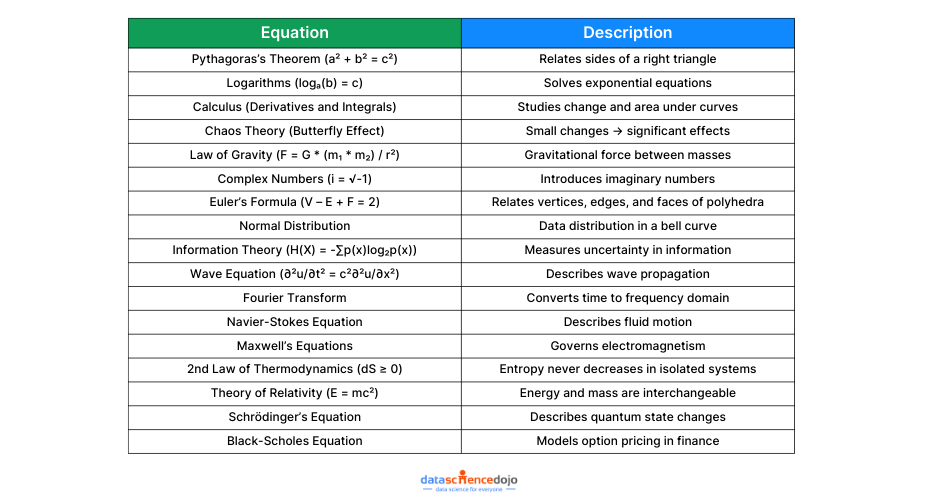
The world we live in is defined by numbers and equations. From the simplest calculations to the most complex scientific theories, equations are the threads that weave the fabric of our understanding.
In this blog, we will step on a journey through the corridors of mathematical and scientific history, where we encounter the most influential equations that have shaped the course of human knowledge and innovation.
These equations are not mere symbols on a page; they are the keys that unlocked the mysteries of the universe, allowed us to build bridges that span great distances, enabled us to explore the cosmos, and even predicted the behavior of financial markets.
Get into the worlds of geometry, physics, mathematics, and more, to uncover the stories behind these 17 equations. From Pythagoras’s Theorem to the Black-Scholes Equation, each has its own unique tale, its own moment of revelation, and its own profound impact on our lives.
Geometry and Trigonometry:
1. Pythagoras’s Theorem
Formula: a^2 + b^2 = c^2
Pythagoras’s Theorem is a mathematical formula that relates the lengths of the three sides of a right triangle. It states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
Also explore: Math for Machine Learning
Example:
Suppose you have a right triangle with two sides that measure 3 cm and 4 cm. To find the length of the hypotenuse, you would use the Pythagorean Theorem:
a^2 + b^2 = c^2
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2
c = 5
Therefore, the hypotenuse of the triangle is 5 cm.
Pythagoras’s Theorem is used in many different areas of work, including construction, surveying, and engineering. It is also used in everyday life, such as when measuring the distance between two points or calculating the height of a building.
Mathematics:
2. Logarithms
Formula: log(a, b) = c
Logarithms are a mathematical operation that is used to solve exponential equations. They are also used to scale numbers and compress data.
Example: Suppose you want to find the value of x in the following equation:2^x = 1024You can use logarithms to solve this equation by taking the logarithm of both sides:log(2^x, 2) = log(1024, 2)x * log(2, 2) = 10 * log(2, 2)x = 10Therefore, the value of x is 10.Logarithms are used in many different areas of work, including finance, engineering, and science.
They are also used in everyday life, such as when calculating interest rates or converting units.
3. Calculus
Calculus is a branch of mathematics that deals with rates of change. It is used to solve problems in many different areas of work, including physics, engineering, and economics.
One of the most important concepts in calculus is the derivative. The derivative of a function measures the rate of change of the function at a given point.
Another important concept in calculus is the integral. The integral of a function is the sum of the infinitely small areas under the curve of the function.
Example:
Suppose you have a function that represents the distance you have traveled over time. The derivative of this function would represent your speed. The integral of this function would represent your total distance traveled.
Calculus is a powerful tool that can be used to solve many different types of problems. It is used in many different areas of work, including science, engineering, and economics.
4. Chaos Theory
Chaos theory is a branch of mathematics that studies the behavior of dynamic systems. It is used to model many different types of systems, such as the weather, the stock market, and the human heart.
One of the most important concepts in chaos theory is the butterfly effect. The butterfly effect states that small changes in the initial conditions of a system can lead to large changes in the long-term behavior of the system.
Example:
Suppose you have a butterfly flapping its wings in Brazil. This could cause a small change in the atmosphere, which could eventually lead to a hurricane in Florida.
Chaos theory is used in many different areas of physics, engineering, and economics. It is also used in everyday life, such as when predicting the weather and managing financial risks.
Learn about the Top 7 Statistical Techniques
Physics:
5. Law of Gravity
Formula: F = G * (m1 * m2) / r^2
The law of gravity is a physical law that describes the gravitational force between two objects. It states that the force between two objects is proportional to the product of their masses and inversely proportional to the square of the distance between them.
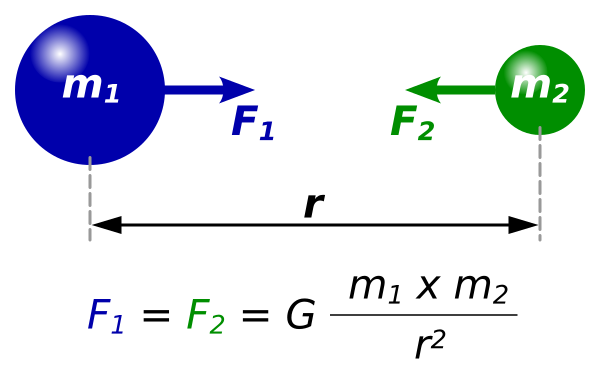
Example:
Suppose you have two objects, each with a mass of 1 kg. The gravitational force between the two objects would be 6.67 x 10^-11 N.
If you double the distance between the two objects, the gravitational force between them would be halved.
The law of gravity is used in many different areas of work, including astronomy, space exploration, and engineering. It is also used in everyday life, such as when calculating the weight of an object or the trajectory of a projectile.
Complex Numbers
6.The square root of minus one
Formula: i = sqrt(-1)
The square root of minus one is a complex number that is denoted by the letter i. It is defined as the number that, when multiplied by itself, equals -1.
Example:
i * i = -1
The square root of minus one is used in many different areas of mathematics, physics, and engineering. It is also used in everyday life, such as when calculating the voltage and current in an electrical circuit.
Read the Top 10 Statistics Books for Data Science
Geometry and Topology
7. Euler’s Formula for Polyhedra
Formula: V – E + F = 2
Euler’s formula for polyhedra is a mathematical formula that relates the number of vertices, edges, and faces of a polyhedron. It states that the number of vertices minus the number of edges plus the number of faces is always equal to 2.
Example:
Suppose you have a cube. A cube has 8 vertices, 12 edges, and 6 faces. If you plug these values into Euler’s formula, you get:
V – E + F = 2
8 – 12 + 6 = 2
Therefore, Euler’s formula is satisfied.
Statistics and Probability:
8. Normal Distribution
9. Information Theory
Formula: H(X) = -∑p(x) log2(p(x))
Information theory is a branch of mathematics that studies the transmission and processing of information. It was developed by Claude Shannon in the mid-20th century.
One of the most important concepts in information theory is entropy. Entropy is a measure of the uncertainty in a message. The higher the entropy of a message, the more uncertain it is.
Example:
Suppose you have a coin. The entropy of the coin is 1 bit, because there are two equally likely outcomes: heads or tails.
If you flip the coin and it lands on heads, the entropy of the coin is 0, because there is only one possible outcome: heads.
Information theory is used in many different areas of communication, computer science, and statistics. It is also used in everyday life, such as when designing data compression algorithms and communication protocols.
Another interesting article on probability distribution
Physics and Engineering:
10. Wave Equation
Formula: ∂^2u/∂t^2 = c^2 * ∂^2u/∂x^2
The wave equation is a differential equation that describes the propagation of waves. It is used to model many different types of waves, such as sound waves, light waves, and water waves.
Example:
Suppose you throw a rock into a pond. The rock will create a disturbance in the water that will propagate outwards in the form of a wave. The wave equation can be used to model the propagation of this wave.
The wave equation is used in many different areas of physics, engineering, and computer science. It is also used in everyday life, such as when designing sound systems and optical devices.
Learn about Top Machine Learning Algorithms for Data Science
11. Fourier Transform
Formula: F(u) = ∫ f(x) * exp(-2pii*ux) dx
The Fourier transform is a mathematical operation that transforms a function from the time domain to the frequency domain. It is used to analyze signals and images.
Example:
Suppose you have a sound recording. The Fourier transform of the sound recording can be used to identify the different frequencies that are present in the recording. This information can then be used to compress the recording or to remove noise from the recording.
The Fourier transform is used in many different areas of science and engineering. It is also used in everyday life, such as in digital signal processing and image processing.
You might also like: Probability Essentials for Data Science
12. Navier-Stokes Equation
Formula: ρ * (∂u/∂t + (u ⋅ ∇)u) = -∇p + μ∇^2u + F
The Navier-Stokes equations are a system of differential equations that describe the motion of fluids. They are used to model many different types of fluid flow, such as the flow of air around an airplane wing and the flow of blood through the body.
Example:
Suppose you are designing an airplane wing. You can use the Navier-Stokes equations to simulate the flow of air around the wing and to determine the lift and drag forces that the wing will experience.
The Navier-Stokes equations are used in many different areas of engineering, such as aerospace engineering, mechanical engineering, and civil engineering. They are also used in physics and meteorology.
13. Maxwell’s Equations
Formula: ∇⋅E = ρ/ε0 | ∇×E = -∂B/∂t | ∇⋅B = 0 | ∇×B = μ0J + μ0ε0∂E/∂t
Maxwell’s equations are a set of four equations that describe the behavior of electric and magnetic fields. They are used to model many different phenomena, such as the propagation of light waves and the operation of electrical devices.
Example:
Suppose you are designing a generator. You can use Maxwell’s equations to simulate the flow of electric and magnetic fields in the generator and to determine the amount of electricity that the generator will produce.
Maxwell’s equations are used in many different areas of physics and engineering. They are also used in everyday life, such as in the design of electrical devices and communication systems.
14. Second Law of Thermodynamics
Formula: dS ≥ 0
The second law of thermodynamics states that the total entropy of an isolated system can never decrease over time. Entropy is a measure of the disorder of a system.
Example:
Suppose you have a cup of hot coffee. The coffee is initially ordered, with the hot molecules at the top of the cup and the cold molecules at the bottom of the cup. Over time, the coffee will cool down and the molecules will become more disordered. This is because the second law of thermodynamics requires the total entropy of the system to increase over time.
The second law of thermodynamics is used in many different areas of physics, engineering, and economics. It is also used in everyday life, such as when designing power plants and refrigerators.
Physics and Cosmology:
15. Relativity
Formula: E = mc^2
Relativity is a branch of physics that studies the relationship between space and time. It was developed by Albert Einstein in the early 20th century. One of the most famous equations in relativity is E = mc^2, which states that energy and mass are equivalent. This means that energy can be converted into mass and vice versa.
Example: Suppose you have a nuclear reactor. The nuclear reactor converts nuclear energy into mass. This is because the nuclear reactor converts the energy of the nuclear binding force into mass. Relativity is used in many different areas of physics, astronomy, and engineering. It is also used in everyday life, such as in the design of GPS systems and particle accelerators.
16. Schrödinger’s Equation
Formula: iℏ∂ψ/∂t = Hψ
Schrödinger’s equation is a differential equation that describes the behavior of quantum mechanical systems. It is used to model many different types of quantum systems, such as atoms, molecules, and electrons.
Example:
Suppose you have a hydrogen atom. The Schrödinger equation can be used to calculate the energy levels of the hydrogen atom and the probability of finding the electron in a particular region of space.
Schrödinger’s equation is used in many different areas of physics, chemistry, and materials science. It is also used in the development of new technologies, such as quantum computers and quantum lasers.
Finance and Economics:
17. Black-Scholes Equation
Formula: ∂C/∂t + ½σ^2S^2∂^2C/∂S^2 – rC = 0
The Black-Scholes equation is a differential equation that describes the price of a European option. A European option is a financial contract that gives the holder the right, but not the obligation, to buy or sell an asset at a certain price on a certain date.
The Black-Scholes equation is used to price options and to develop hedging strategies. It is one of the most important equations in finance.
Example:
Suppose you are buying a call option on a stock. The Black-Scholes equation can be used to calculate the price of the call option. This information can then be used to decide whether or not to buy the call option and to determine how much to pay for it.
The Black-Scholes equation is used by many different financial institutions, such as investment banks and hedge funds. It is also used by individual investors to make investment decisions.
Share Your Favorite Equation With Us!
Mathematics and science are not just abstract concepts but the very foundations upon which our modern world stands. These 17 equations have not only changed the way we see the world but have also paved the way for countless innovations and advancements.
From the elegance of Euler’s Formula for Polyhedra to the complexity of Maxwell’s Equations, from the order of Normal Distribution to the chaos of Chaos Theory, each equation has left an indelible mark on the human story.
They have transcended their origins and become tools that shape our daily lives, drive technological progress, and illuminate the mysteries of the cosmos.
As we continue to explore, learn, and discover, let us always remember the profound impact of these equations and the brilliant minds behind them. They remind us that the pursuit of knowledge knows no bounds and that the world of equations is a realm of infinite wonder and possibility.
Let us know in the comments in case we missed any!