The Poisson Process Unveiled: Definition & Key Properties

The Poisson process is a popular method of counting random events that occur at a certain rate. It is commonly used in situations where the timing of events appears to be random, but the rate of occurrence is known. For example, the frequency of earthquakes in a specific region or the number of car accidents at a location can be modeled using the Poisson process. 

 

Understanding the Parameters of the Poisson Process

The Poisson process is defined by several key properties: 

• Events happen at a steady rate over time 

• The probability of an event happening in a short period of time is inversely proportional to the duration of the interval, and 
• Events take place independently of one another.  

Additionally, the Poisson distribution governs the number of events that take place during a specific period, and the rate parameter (which determines the mean and variance) is the only parameter that can be used to describe it. 

Mathematical Definition of the Poisson Process

To calculate the probability of a given number of events occurring in a Poisson process, the Poisson distribution formula is used: P(x) = (lambda^x * e^(-lambda)) / x! where lambda is the rate parameter and x! is the factorial of x. 

The Poisson process can be applied to a wide range of real-world situations, such as the arrival of customers at a store, the number of defects in a manufacturing process, the number of calls received by a call center, the number of accidents at a particular intersection, and the number of emails received by a person in a given time-period.  

It’s essential to keep in mind that the Poisson process is a stochastic process that counts the number of events that have occurred in a given interval of time, while the Poisson distribution is a discrete probability distribution that describes the likelihood of events with a Poisson process happening in a given time-period.

 

 

Real Scenarios To Use the Poisson Process

The Poisson process is a popular counting method used in situations where events occur at a certain rate but are actually random and without a certain structure. It is frequently used to model the occurrence of events over time, such as the number of faults in a manufacturing process or the arrival of customers at a store. Some examples of real-life situations where the Poisson process can be applied include: 

• The arrival of customers at a store or other business: The rate at which customers arrive at a store can be modeled using a Poisson process, with the rate parameter representing the average number of customers that arrive per unit of time. 
• The number of defects in a manufacturing process: The rate at which defects occur in a manufacturing process can be modeled using a Poisson process, with the rate parameter representing the average number of defects per unit of time. 
• The number of calls received by a call center: The rate at which calls are received by a call center can be modeled using a Poisson process, with the rate parameter representing the average number of calls per unit of time. 
• The number of accidents at a particular intersection: The rate at which accidents occur at a particular intersection can be modeled using a Poisson process, with the rate parameter representing the average number of accidents per unit of time. 
• The number of emails received by a person in a given time period: The rate at which emails are received by a person can be modeled using a Poisson process, with the rate parameter representing the average number of emails received per unit of time. 

It’s also used in other branches of probability and statistics, including the analysis of data from experiments involving a large number of trials and the study of queues. 

Poisson Process Variants: Non-Homogeneous Poisson Process (NHPP)

While the standard Poisson process assumes a constant rate (λ) over time, many real-world scenarios involve event rates that change dynamically. This leads to the Non-Homogeneous Poisson Process (NHPP), where the rate function λ(t) varies instead of staying fixed.

How NHPP Works

In an NHPP, the probability of an event occurring depends on time-varying intensity rather than a fixed average rate. Instead of using a constant λ, the process follows a function λ(t) that defines how the intensity changes over time.

The cumulative intensity function, called the mean value function Λ(t), is calculated as:

Λ(t)=∫0tλ(u) du\Lambda(t) = \int_0^t \lambda(u) \, duΛ(t)=∫0t​λ(u)du

This integral determines the expected number of events up to time t.

Applications of NHPP

1. Finance – NHPP models fluctuations in stock market transactions, where trading activity is higher during market openings and closings.
2. Healthcare – Used to model disease outbreaks where infection rates vary seasonally or due to interventions.
3. Weather Forecasting – Applied to rainfall modeling, where storm intensity fluctuates over time rather than occurring at a constant rate.
4. Network Traffic – Internet and telecommunications traffic often peaks during certain hours, making NHPP useful in modeling call volumes and data requests.

Simulating NHPP

NHPP can be simulated by dividing time into small intervals and adjusting the event probability based on λ(t). A common approach is thinning, where candidate event times from a standard Poisson process are filtered based on the varying rate function.

Why NHPP Matters

Unlike the traditional Poisson process, NHPP provides flexibility in modeling real-world situations where event occurrences are not uniform. It helps in better forecasting, risk analysis, and resource planning, making it a crucial tool in fields dealing with dynamic event rates.

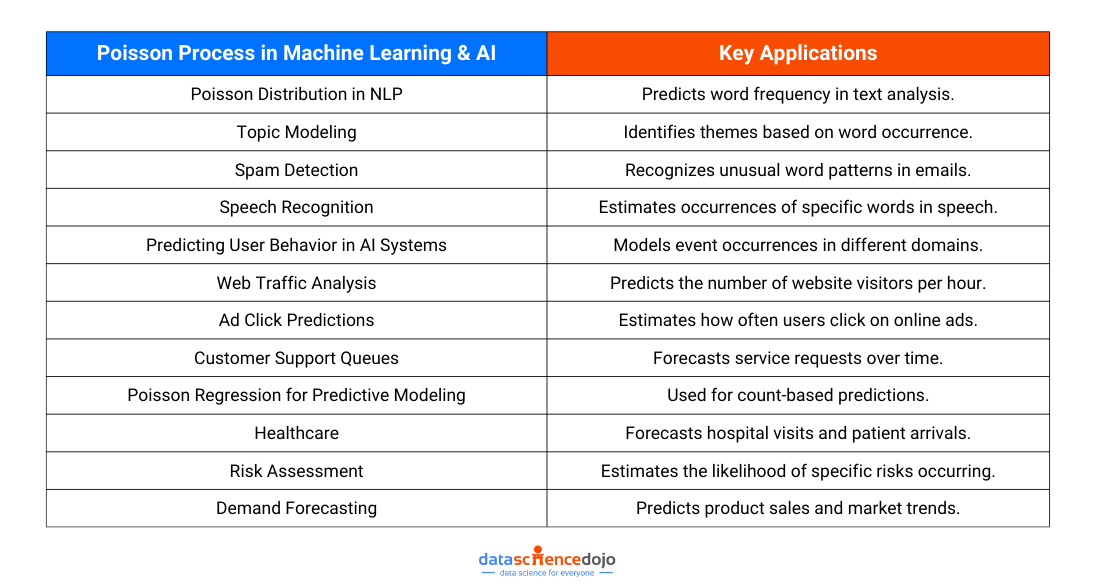
Poisson Process in Machine Learning & AI

In machine learning and AI, many real-world problems involve predicting how often an event will occur within a fixed time or space. This is where the Poisson distribution becomes useful, as it models the probability of a given number of events happening in a fixed interval. From natural language processing (NLP) to recommendation systems, Poisson-based models help make sense of count-based data and improve predictive accuracy.

Poisson Distribution in NLP

One key application of the Poisson distribution is in text analysis, where it helps predict how often a word appears in a document. Rare words tend to follow a Poisson-like distribution, making this useful for:

• Topic Modeling – Identifying themes based on word frequency.
• Spam Detection – Recognizing unusual word patterns in spam emails.
• Speech Recognition – Estimating the occurrence of specific words in spoken language.

Predicting User Behavior in AI Systems

AI-powered systems often rely on Poisson processes to model event occurrences in various domains:

• Web Traffic Analysis – Predicting the number of visitors per hour on a website.
• Ad Click Predictions – Estimating how often users will click on an online ad.
• Customer Support Queues – Forecasting the number of service requests in a given period.

Poisson Regression for Predictive Modeling

Poisson regression is a valuable technique when dealing with count-based predictions, such as forecasting the number of hospital visits, sales transactions, or social media shares. Unlike linear regression, which assumes continuous outcomes, Poisson regression is tailored for non-negative integer outputs, making it ideal for applications in healthcare, risk assessment, and demand forecasting.

By incorporating the Poisson process into machine learning models, AI systems can better predict how often an event will happen, leading to more accurate and data-driven decision-making.

 

 

Limitations of the Poisson Process

The Poisson process is a useful tool for modeling random events, but it comes with several limitations that can affect its accuracy in real-world applications. Here are some key constraints to keep in mind:

• Independence of Events – Assumes events occur independently, but real-world events are often correlated (e.g., aftershocks following an earthquake).
• No Simultaneous Events – It does not allow multiple events to happen at the exact same time, which is unrealistic in many systems (e.g., network traffic congestion).
• Memoryless Property – Assumes the time until the next event is independent of past events, which is not true for systems where past occurrences influence future ones (e.g., machine wear and tear).
• Limited to Rare Events – Works best for rare events and may not be accurate for high-frequency occurrences (e.g., peak-hour internet traffic).
• Homogeneity in Space – Assumes events occur uniformly in time but does not account for spatial variability (e.g., earthquake epicenter distribution).
• Inability to Model Overdispersion – Assumes variance equals the mean, but many real-world datasets have greater variability (e.g., fluctuating insurance claims).
• Limited to Countable Events – Cannot model continuous data, making it unsuitable for non-discrete phenomena (e.g., rainfall intensity).
• Sensitivity to Time Intervals – Assumes a constant event rate, but real-world event rates often vary over time (e.g., hospital patient arrivals between shifts).
• No Accommodation for External Factors – Does not account for external influences affecting event rates (e.g., vaccination rates impacting disease spread).

Wrapping Up

The Poisson process is a powerful tool for modeling events that happen at a certain average rate but in a random manner. It is defined by a constant event rate, independence between events, and an inverse relationship between interval length and event probability.

The Poisson distribution helps calculate the probability of a given number of events occurring in a fixed time frame. This makes it useful for real-world applications like customer arrivals, manufacturing defects, call center activity, and traffic accidents.

In machine learning and AI, the Poisson process is key for count-based predictions. It helps model word frequencies in NLP, user interactions in recommendation systems, and web traffic trends. Poisson regression is widely used in healthcare, finance, and marketing to predict event occurrences.

By integrating the Poisson process into analytics and AI, we can better understand event patterns and make data-driven decisions. Whether in queueing systems, risk assessment, or demand forecasting, it remains a fundamental concept in probability and statistics.