The Monte Carlo method is a technique for solving complex problems using probability and random numbers. Through repeated random sampling, Monte Carlo calculates the probabilities of multiple possible outcomes occurring in an uncertain process.
Whenever you try to solve problems in the future, you make certain assumptions. For example, forecasting problems make certain assumptions like the cost of a particular item, the value of stocks, or electricity units used in the future. Since these problems try to predict an estimate of an unknown value based on historical data, there always exists inherent risk and uncertainty.
The Monte Carlo simulation allows us to see all the possible outcomes of our decisions and assess risk, consequently allowing for better decision-making under uncertainty.
This blog will walk through the famous Monty Hall problem, and how it can be solved using the Monte Carlo method using Python.
Monty Hall problem
In the Monty Hall problem, the TV show host Monty presents three doors to the participant. Behind one of the doors is a valuable prize like a car, while behind the others is a less valuable prize like a goat.
Consider yourself to be one of the participants in the show. You choose one out of the three doors. Before opening your chosen door, Monty opens another door behind which would be one of the goats. Now you are left with two doors, behind one could be the car, and behind the other would be the other goat.
Monty then gives you the option to either switch your answer to the other unopened door or stick to the original one.
Is it in your favor to switch your answer to the other door? Well, probability says it is!
Let’s see how:
Initially, there are three unopen doors in front of you. The probability of the car being behind any of these doors is 1/3.
Let’s say you decide to pick door #1 as the probability is the same (1/3) for each of these doors. In other words, the probability that the car is behind door #1 is 1/3, and the probability that it will be behind either door #2 or door #3 is 2/3.
Monty is aware of the prize behind each door. He chooses to open door #3 and reveal a goat. He then asks you if you would like to either switch to door #2 or stick with door #1.

To solve the problem, let’s switch to Python and apply the Monte Carlo simulation.
Solving with Python
Initialize the 3 prizes

Create python lists to store the probabilities after each game. We will play as many games as iterations input.

Monte Carlo simulation
Before starting the game, we randomize the prizes behind each door. One of the doors will have a car behind it, while the other two will have a goat each. When we play a large number of games, all possible permutations get covered of prize distributions, and door choices get covered.

Below is the code that decides if your choice was correct or not, and if switching would’ve been the correct move.

After playing each game, the winning probabilities are updated and stored in the lists. When all games have been played, we return the final values of each of the lists, i.e., winning by switching your choice and winning by sticking to your choice.

Get results
Enter your desired number of iterations (the higher the number, the more numbers of games will be played to approximate the probabilities). In the final step, plot your results.

After running the simulation 1000 times, the probability that we win by always switching is 67.7%, and the probability that we win by always sticking to our choice is 32.3%. In other words, you will win approximately 2/3 times if you switch your door, and only 1/3 times if you stick to the original door.
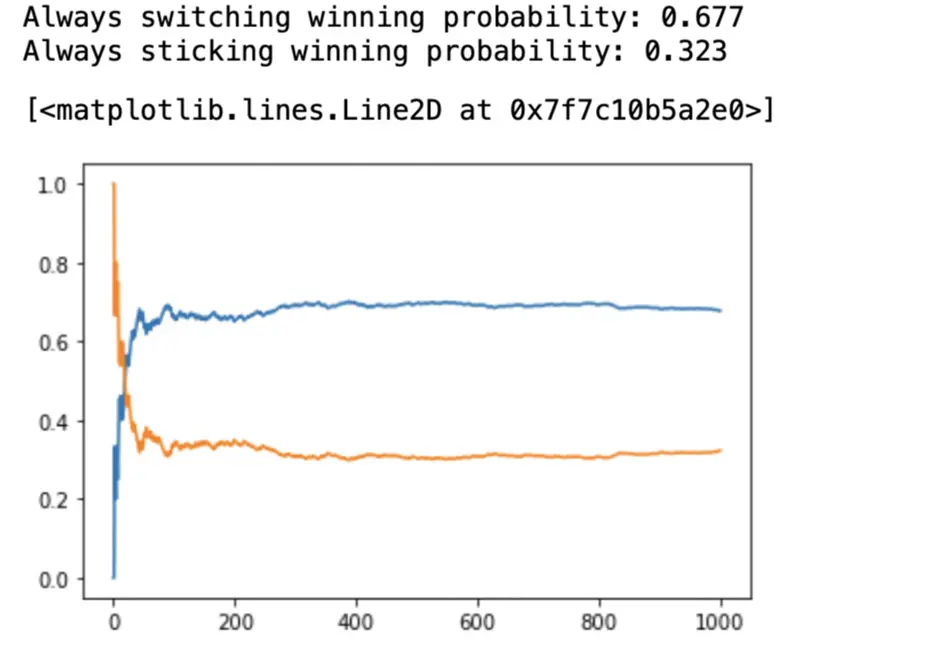
Therefore, according to the Monte Carlo simulation, we are confident that it works to our advantage to switch the door in this tricky game.
Written by Aadam Nadeem




