In the world of data analysis, drawing insights from a limited dataset can often be challenging. Traditional statistical methods sometimes fall short when it comes to deriving reliable estimates, especially with small or skewed datasets. This is where bootstrap sampling, a powerful and versatile statistical technique, comes into play.
In this blog, we’ll explore what bootstrap sampling is, how it works, and its various applications in the field of data analysis.
What is Bootstrap Sampling?
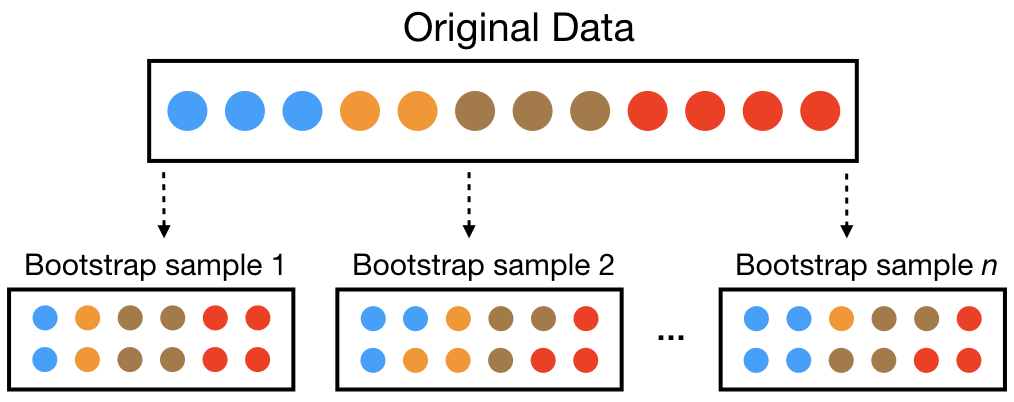
Bootstrap sampling is a resampling method that involves repeatedly drawing samples from a dataset with replacements to estimate the sampling distribution of a statistic.
Essentially, you take multiple random samples from your original data, calculate the desired statistic for each sample, and use these results to infer properties about the population from which the original data was drawn.
Learn about boosting algorithms in machine learning
Why do we Need Bootstrap Sampling?
This is a fundamental question I’ve seen machine learning enthusiasts grapple with. What is the point of bootstrap sampling? Where can you use it? Let me take an example to explain this.
Let’s say we want to find the mean height of all the students in a school (which has a total population of 1,000). So, how can we perform this task?
One approach is to measure the height of a random sample of students and then compute the mean height. I’ve illustrated this process below.
Traditional Approach
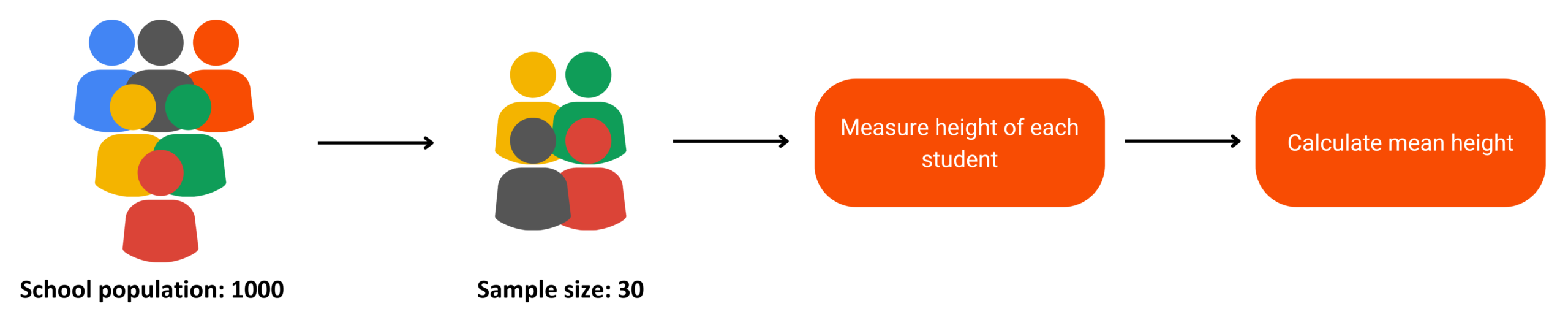
- Draw a random sample of 30 students from the school.
- Measure the heights of these 30 students.
- Compute the mean height of this sample.
However, this approach has limitations. The mean height calculated from this single sample might not be a reliable estimate of the population mean due to sampling variability. If we draw a different sample of 30 students, we might get a different mean height.
Another interesting read: Machine Learning techniques
To address this, we need a way to assess the variability of our estimate and improve its accuracy. This is where bootstrap sampling comes into play.
Bootstrap Approach

- Draw a random sample of 30 students from the school and measure their heights. This is your original sample.
- From this original sample, create many new samples (bootstrap samples) by randomly selecting students with replacements. For instance, generate 1,000 bootstrap samples.
- For each bootstrap sample, calculate the mean height.
- Use the distribution of these 1,000 bootstrap means to estimate the mean height of the population and to assess the variability of your estimate.
Implementation in Python
To illustrate the power of bootstrap sampling, let’s calculate a 95% confidence interval for the mean height of students in a school using Python. We will break down the process into clear steps.
Step 1: Import Necessary Libraries
First, we need to import the necessary libraries. We’ll use `numpy` for numerical operations and `matplotlib` for visualization.
Step 2: Create the Original Sample
We will create a sample dataset of heights. In a real-world scenario, this would be your collected data.
Step 3: Define the Bootstrap Function
We define a function that generates bootstrap samples and calculates the mean for each sample.
- data: The original sample.
- n_iterations: Number of bootstrap samples to generate.
- -bootstrap_means: List to store the mean of each bootstrap sample.
- -n_size: The original sample’s size will be the same for each bootstrap sample.
- -np.random.choice: Randomly select elements from the original sample with replacements to create a bootstrap sample.
- -sample_mean: Mean of the bootstrap sample.
Explore the use of Gini Index and Entropy in data analytics
Step 4: Generate Bootstrap Samples
We use the function to generate 1,000 bootstrap samples and calculate the mean for each.
Step 5: Calculate the Confidence Interval
We calculate the 95% confidence interval from the bootstrap means.
- np.percentile: Computes the specified percentile (2.5th and 97.5th) of the bootstrap means to determine the confidence interval.
Step 6: Visualize the Bootstrap Means
Finally, we can visualize the distribution of bootstrap means and the confidence interval.
- plt.hist: Plots the histogram of bootstrap means.
- plt.axvline: Draws vertical lines for the confidence interval.
By following these steps, you can use bootstrap sampling to estimate the mean height of a population and assess the variability of your estimate. This method is simple yet powerful, making it a valuable tool in statistical analysis and data science.
Read about ensemble methods in machine learning
Applications of Bootstrap Sampling
Bootstrap sampling is widely used across various fields, including the following:
Economics
Bootstrap sampling is a versatile tool in economics. It excels in handling non-normal data, commonly found in economic datasets. Key applications include constructing confidence intervals for complex estimators, performing hypothesis tests without parametric assumptions, evaluating model performance, and assessing financial risk.
For instance, economists use bootstrap to estimate income inequality measures, analyze macroeconomic time series, and evaluate the impact of economic policies. The technique is also used to estimate economic indicators, such as inflation rates or GDP growth, where traditional methods might be inadequate.
You might also like: GenAI for Data Analytics
Medicine
Bootstrap sampling is applied in medicine to analyze clinical trial data, estimate treatment effects, and assess diagnostic test accuracy. It helps in constructing confidence intervals for treatment effects, evaluating the performance of different diagnostic tests, and identifying potential confounders.
Bootstrap can be used to estimate survival probabilities in survival analysis and to assess the reliability of medical imaging techniques. It is also suitable to assess the reliability of clinical trial results, especially when sample sizes are small or the data is not normally distributed.
Also look at: Healthcare Data Exploration in Tableau
Machine Learning
In machine learning, bootstrap estimates model uncertainty, improves model generalization, and selects optimal hyperparameters. It aids in tasks like constructing confidence intervals for model predictions, assessing the stability of machine learning models, and performing feature selection.
Bootstrap can create multiple bootstrap samples for training and evaluating different models, helping to identify the best-performing model and prevent overfitting. For instance, it can evaluate the performance of predictive models through techniques like bootstrapped cross-validation.
Ecology
Ecologists utilize bootstrap sampling to estimate population parameters, assess species diversity, and analyze ecological relationships. It helps in constructing confidence intervals for population means, medians, or quantiles, estimating species richness, and evaluating the impact of environmental factors on ecological communities.
Bootstrap is also employed in community ecology to compare species diversity between different habitats or time periods.
Advantages and Disadvantages
| Advantages
|
Disadvantages
|
| Non-parametric Method: No assumptions about the underlying distribution of the data, making it highly versatile for various types of datasets. | Computationally Intensive: Requires many resamples, which can be computationally expensive, especially with large datasets.
|
| Flexibility: Can be used with a wide range of statistics and datasets, including complex measures like regression coefficients and other model parameters. | Not Always Accurate: May not perform well with very small sample sizes or highly skewed data. The quality of the bootstrap estimates depends on the original sample representative of the population.
|
| Simplicity: Conceptually straightforward and easy to implement with modern computational tools, making it accessible even for those with basic statistical knowledge. | Outlier Sensitivity: Bootstrap sampling can be affected by outliers in the original data. Since the method involves sampling with replacement, outliers can appear multiple times in bootstrap samples, potentially biasing the estimated statistics. |
To Sum it Up
Bootstrap sampling is a powerful tool for data analysis, offering flexibility and practicality in a wide range of applications. By repeatedly resampling from your dataset and calculating the desired statistic, you can gain insights into the variability and reliability of your estimates, even when traditional methods fall short.
Whether you’re working in economics, medicine, machine learning, or ecology, understanding and utilizing bootstrap sampling can enhance your analytical capabilities and lead to more robust conclusions.








